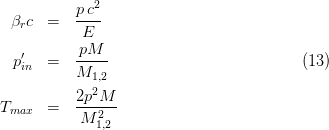As treated in [Boschini et al. (2011)], at small distances from the nucleus, the
potential energy is a Coulomb potential, while - at distances larger than the Bohr
radius - the nuclear field is screened by the fields of atomic electrons. The
interaction between two nuclei is usually described in terms of an interatomic
Coulomb potential (e.g., see Sections 2.2.1 and 2.2.2 of [Leroy and Rancoita
(2016)] and Section 4.1 of [ICRU Report 49 (1993)]), which is a function of the
radial distance r between the two nuclei
where ez (projectile) and eZ (target) are the charges of the bare nuclei and ΨI is
the interatomic screening function. This latter function depends on the reduced
radius rr given by
where aI is the so-called screening length (also termed screening radius). In the
framework of the Thomas–Fermi model of the atom (e.g., see Chapters 1 and 2
of [Torrens (1972)]) - thus, following the approach of [ICRU Report 49 (1993)] -,
a commonly used screening length for z = 1 incoming particles is that from
Thomas–Fermi (e.g., see [Thomas (1927), Fermi (1928)])
and - for incoming particles with z ≥ 2 - that introduced by [Ziegler,
Biersack and Littmark (1985)] (and termed universal screening
length1)
where
is the Bohr radius, m is the electron rest mass and
is a constant introduced in the Thomas–Fermi model. The simple scattering
model due to [Wentzel (1926)] - with a single exponential screening-function
ΨI(rr) {e.g., see [Wentzel (1926)] and Equation (21) in [Fernandez-Varea et
al. (1993)]} - was repeatedly employed in treating single and multiple
Coulomb-scattering with screened potentials (e.g., see [Fernandez-Varea et al.
(1993)] - and references therein - for a survey of such a topic and also [Molière
(1947, 1948), Bethe (1953), Butkevick et al. (2002), Boschini et al. (2010)]). The
resulting elastic differential cross section differs from the Rutherford differential
cross section by an additional term - the so-called screening parameter -
which prevents the divergence of the cross section when the angle θ of
scattered particles approaches 0∘. The screening parameter A
s,M [e.g., see
Equation (21) of [Bethe (1953)])] - as derived in [Molière (1947, 1948)]
for the single Coulomb scattering using a Thomas–Fermi potential - is
expressed2
as
where aI is the screening length - from Eqs. (3, 4) for particles with z = 1 and
z ≥ 2, respectively; α is the fine-structure constant; p (βc) is the momentum
(velocity) of the incoming particle undergoing the scattering onto a target
supposed to be initially at rest; c and ℏ are the speed of light and the
reduced Planck constant, respectively. When the (relativistic) mass - with
corresponding rest mass m - of the incoming particle is much lower than
the rest mass (M) of the target nucleus, the differential cross section -
obtained from the Wentzel–Molière treatment of the single scattering - is:
Thus, for β ≃ 1 (i.e., at very large p) and with As,M ≪ 1, from Eqs. (5, 8) one
finds that the cross section approaches a constant:
In case of a scattering under the action of a central potential (for instance that
due to a screened Coulomb field), when the rest mass of the target particle is no
longer much larger than the relativistic mass of the incoming particle, the
expression of the differential cross section must properly be re-written - in the
center of mass system - in terms of an “effective particle” with momentum (pr′)
equal to that of the incoming particle (p′in) and rest mass equal to the relativistic
reduced mass
where M1,2 is the invariant mass; m and M are the rest masses of the incoming
and target particles, respectively (e.g., see [Boschini et al. (2010), Fiziev and Todorov (2001), Starusziewicz
and Zalewski (1977)] and references therein). The
“effective particle” velocity is given by:
Thus, above 50 keV/nucleon (e.g., see here) the differential cross section3
per unit solid angle of the incoming particle results to be given by
with
θ′ the scattering angle in the center of mass system and with the screening parameter further discussed in Eq. (5) here. Furthermore (e.g., see Section 2.2.2 of [Leroy and Rancoita (2016)]), assuming
an isotropic azimuthal distribution one can re-write Eq. (10) in terms
of the kinetic energy transferred from the projectile to the recoil target
as:
Furthermore, since Therefore, Eq. (12) can be re-written as
Equation (14) expresses - as already mentioned - the differential cross section as a
function of the (kinetic) energy T achieved by the recoil target.
[Agostinelli et al., Geant4 (2003)] S. Agostinelli et al., Geant4 a
simulation toolkit, Nucl. Instr. and Meth. in Phys. Res. A 506 (2003),
250-303; see also the website: http://geant4.cern.ch/
[Boschini et al. (2010)] M.J. Boschini, C. Consolandi, M. Gervasi, S.Giani, D.Grandi, V. Ivanchenko and P.G. Rancoita, Geant4-based application
development for NIEL calculation in the Space Radiation Environment,
Proc. of the 11th ICATPP Conference, October 5–9 2009, Villa
Olmo, Como, Italy, World Scientific, Singapore (2010), 698–708, IBSN:
10-981-4307-51-3.
[Boschini et al. (2011)] M.J. Boschini, C. Consolandi, M. Gervasi, S. Giani, D. Grandi, V. Ivantchenko, S. Pensotti, P.G. Rancoita, M. Tacconi, Nuclear and
Non-Ionizing Energy-Loss for Coulomb Scattered Particle from Low
Energy up to relativistic regime in Space Radiation Environment, Proc.
of the 12th ICATPP Conference, October 7-8 2010, Villa Olmo,
Como, Italy, World Scientific, Singapore (2011), 9-23, IBSN: 978-981-4329-02-6; http://www.worldscientific.com/doi/pdf/10.1142/9789814329033_0002
or http://arxiv.org/pdf/1011.4822v7.pdf.
[Fiziev and Todorov (2001)] P.P. Fiziev and I.T. Todorov, Phys. Rev. D
63 (2001), 104007-1–104007-9.
[Bethe (1953)] H. A. Bethe, Phys. Rev. 89 (1953), 1256–1266.
[Butkevick et al. (2002)] A. V. Butkevick et al., Nucl. Instr. and Meth.
in Phys. Res. A 488 (2002), 282-194.
[Fermi (1928)] E. Fermi, Z. Phys. 48 (1928), 73–79.
[Fernandez-Varea et al. (1993)] J.M. Fernandez-Varea et al., Nucl. Instr.
and Meth. in Phys. Res. B 73 (1993), 447–473.
[ICRU Report 49 (1993)] ICRU, ICRU Report 49, Stopping Powers and
Ranges for Protons and Alpha Particles (1993).
[Kalbitzer and Oetzmann (1976)] S. Kalbitzer and H. Oetzmann, Phys.
Lett. A 59 (1976), 197–198.
[Leroy and Rancoita (2016)]
C. Leroy and P.G. Rancoita (2016), Principles of Radiation
Interaction in Matter and Detection - 4th Edition -, World Scientific.
Singapore, ISBN-978-981-4603-18-8 (printed); ISBN.978-981-4603-19-5
(ebook); https://www.worldscientific.com/worldscibooks/10.1142/9167#t=aboutBook; it is also partially accessible via google books.
[Lindhard and Sharff (1961)] J. Lindhard and M. Sharff, Phys. Rev. 124
(1961), 128–130.
[Lindhard and Sharff (1961)] J. Lindhard and M. Sharff, Phys. Rev. 124
(1961), 128–130.
[Molière (1947, 1948)] von G. Molière, Z. Naturforsh. A2 (1947),
133–145; A3 (1948), 78.
[Starusziewicz and Zalewski (1977)] A. Starusziewicz and K.
Zalewski Acta Phys. Pol. B 8 (no. 10) (1977), 815–817.
[Thomas (1927)] L.H. Thomas, Proc. Cambridge Phil. Soc. 23 (1927),
542.
[Torrens (1972)] I.M. Torrens, Interatomic Potentials, Academic Press
(New York) 1972.
[Wentzel (1926)] G. Wentzel, Z. Phys. 40 (1926), 590–593.
[Ziegler, Biersack and Littmark (1985)] J.F. Ziegler, J.P. Biersack and U.
Littmark, The Stopping Range of Ions in Solids, Vol. 1, Pergamon Press
(New York) 1985.
1Another screening length commonly used is that from [Lindhard and Sharff (1961)] (see
also [Kalbitzer and Oetzmann (1976)] and references therein):
2It has to be remarked that the screening radius originally used in [Molière (1947,
1948), Bethe (1953)] was that from Eq. (3).
3By inspection of Eqs. (5, 7, 10, 11), one finds that for βr ≊ 1 the cross section is given
by Eq. (9).
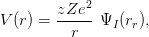
(1)
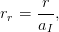
(2)
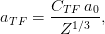
(3)
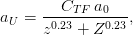
(4) 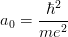
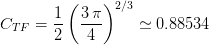
![( )2 [ ( )2]
As,M = --ℏ--- 1.13 + 3.76 × αzZ--
2p aI β](/images/images_handbook/screenedpotentials7x.png)
(5)
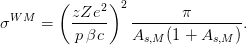
(8)
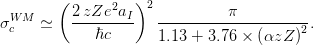
(9) 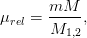
![┌ ------------------
││ [ ( )2 ]-1
βrc = c∘ 1 + μrelc- .
p ′in](/images/images_handbook/screenedpotentials12x.png)
![WM ′ ( 2 )2
dσ----(θ-) -zZe---- --------1---------
dΩ ′ = 2p′inβrc [A + sin2(θ′∕2 )]2,
s](/images/images_handbook/screenedpotentials13x.png)
(10)
![( )2 [ ( )2]
---ℏ---- αzZ--
As = 2 p′in aI 1.13 + 3.76 × βr](/images/images_handbook/screenedpotentials14x.png)
(11)
![( )
dσW-M-(T)- -zZe2-- 2 ----Tmax-------
dT = π p′ β c 2.
in r [Tmax As + T]](/images/images_handbook/screenedpotentials15x.png)
(12) 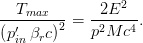
![W M 2
dσ----(T-)= 2π (zZe2 )2--E-----------1-------.
dT p2M c4[Tmax As + T ]2](/images/images_handbook/screenedpotentials18x.png)
(14) References
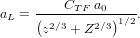
![dσW M (θ) (zZe2 )2 1
--------- = ----- -------------------- (6)
dΩ pβc (2As,M + 1 - cosθ)2
( zZe2 )2 1
= ------ [----------------]2 (7)
2 pβc As,M + sin2(θ∕2)](/images/images_handbook/screenedpotentials8x.png)