Non Ionizing Energy Loss (NIEL) and Displacement Stopping Power
The non-ionizing energy-loss (NIEL) accounts for the amount of energy - lost by a particle passing through a medium -, which was imparted to create atomic displacements. It can be expressed in units of
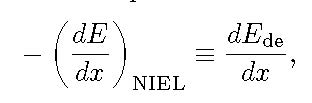
where ![]() is the displacement stopping power (e.g., see discussion in Sect. 4.2.1 of [Leroy and Rancoita (2011)]) and the minus sign indicates that the energy is lost by the incoming particle to create atomic displacements inside the absorber. For instance, in case of (elastic) Coulomb scattering on nuclei, the displacement stopping power can be calculated as
is the displacement stopping power (e.g., see discussion in Sect. 4.2.1 of [Leroy and Rancoita (2011)]) and the minus sign indicates that the energy is lost by the incoming particle to create atomic displacements inside the absorber. For instance, in case of (elastic) Coulomb scattering on nuclei, the displacement stopping power can be calculated as
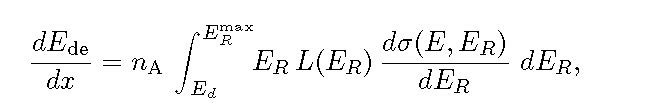
where [see Eq. (1.71) at page 25 of [Leroy and Rancoita (2012)]
![]()
is the number of atoms per cm3 in the absorber, ρA and A are the density and atomic weight of the medium, respectively; N is the Avogadro constant, E is the kinetic energy of the incoming particle; ER and ER max are the recoil kinetic energy and the maximum energy transferred to the recoil nucleus, respectively; Ed is the so-called displacement threshold energy, i.e., the minimum energy necessary to permanently displace an atom from its lattice position; the expression of L(ER) is the Lindhard partition function discussed, for instance, in Sects. 4.2.1 and 4.2.1.2 in [Leroy and Rancoita (2011)] (see also references therein and [Jun (2001)]); finally, dσ(E,ER)/d ER is the differential cross section for elastic Coulomb scattering for electrons or protons or ions on nuclei. Furthermore, the non-ionizing energy-loss (NIEL) can be expressed in units of MeV cm2/g as
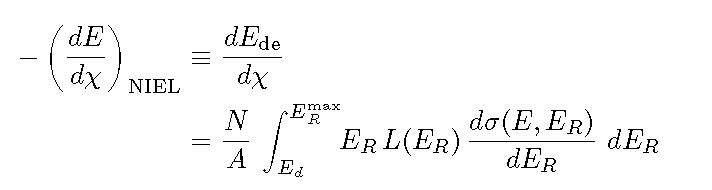
with χ =x ρA, ρA the absorber density in g/cm3 and dEde/dχ the displacement mass-stopping power.
Furthermore, the displacement stopping power can allow one to determine the Dose due to non-ionizing energy loss process (i.e., the NIEL dose).

In the above equation, the medium has to to be thick enough to fully absorb the kinetic energy of recoil nuclei. An analytical approximation of L(ER) - the so-called Norgett-Robinson-Torrens expression - can be found, for instance, in Equations (7.26, 7.27) of Sections 7.1.1.1 and 7.1.1.2 in Leroy and Rancoita (2016) (see also references therein).
In the framework of the screened relativistic NIEL approach, the values of NIEL in units of MeV cm2/g for electrons (e.g., see Sect 2 of [C. Baur et al. (2014)] ) are obtained using the Mott differential cross section [Mott (1929)] of electrons on nuclei calculated from the practical expression discussed in [Boschini et al. (2013)] (see also [Linjian et al. (1995)]) and accounting for the effects due to both screened nuclear potentials and form factors discussed in [Boschini et al. (2012)] and Sects. 1.3.1-1.3.3 of [Leroy and Rancoita (2012)] (see also references therein and the webpage).
Hereafter, (i.e., see Chapter 2 in [Leroy and Rancoita (2016)]) is reported the discussion about the currently implemented form factors in this calculation of the nuclear stopping power and screened relativistic NIEL.

The Coulomb contribution to the overall NIEL for protons and nuclei above 50 keV/nucleon is obtained using the elastic cross section derived from treatment of the nucleus-nucleus screened Coulomb scattering discussed in [Boschini et al. (2011)] and Sect. 2.1.4.2 in [Leroy and Rancoita (2011)] (see also [Fernandez-Varea et al. (1993), Butkevick (2002), Boschini et al. (2010)]). That treatment allows one to deal with a scattering occurring up to relativistic energies.
For energies lower than 50-200 keV/nucleon, the scattering of protons and screened nuclei can be treated using the 4-terms analytical approximation of the ZBL cross section derived by Messenger et al. (2004) [see Eqs. (1--3, 15) and also references therein].
It is worth to note that, in the framework of the screened relativistic treatment, the diplacement stopping power (thus the NIEL) is calculated as a function of the displacement threshold energy (e.g., see Chapers 2, 7 and 8 of [Leroy and Rancoita (2016)]).
Furthermore, for protons in Si and GaAs absorbers, the NIEL contribution resulting from hadronic interactions was estimated, for instance, by Jun et al. (2003) at Ed =10 eV. These authors found that for protons with energies above about 20 (30) MeV this is the dominant NIEL process - with respect to that due to elastic Coulomb scattering - in a Si (GaAs) absorber. A discussion about this topic can be found in Sect. 4.2.1.4 of [Leroy and Rancoita (2011)]) and Chapter 7 in [Leroy and Rancoita (2016)].
In the present NIEL calculators, for protons up to 1 GeV and alpha-particles up to 1 GeV/nucleon impinging on elements with atomic number from Z=4 up to Z=51 , the hadronic contributions were interpolated or extrapolated from those obtained from [Jun et al. (2003, 2004),Jun (2017)] regarding 10 absobers. For silicon absorbers, in addition, the hadronic contribution for energier from 1 up to 24 GeV was obtatined from [Huhtinen (2002)].
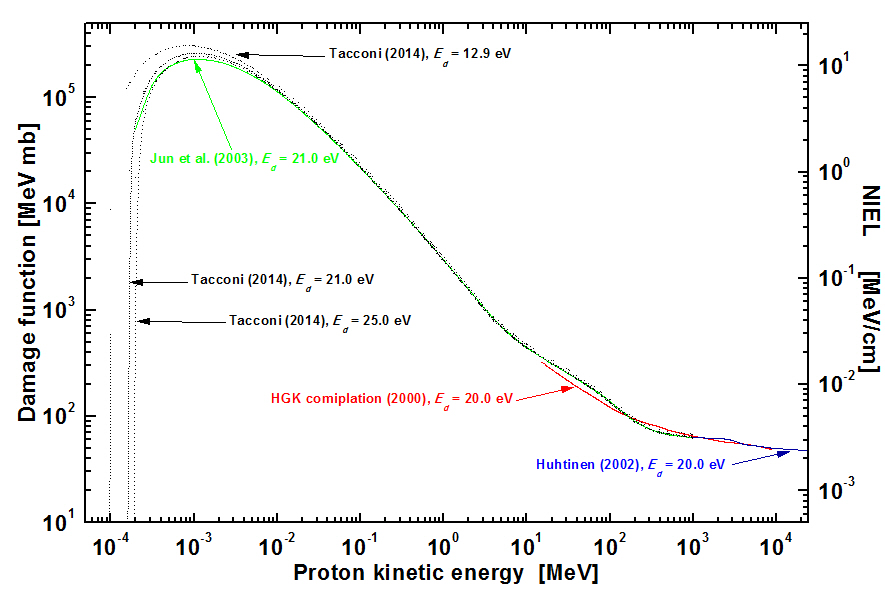
Further discussions on hadronic NIEL contributions and references to literature are available in Sects. 7.1.2-7.1.2.2 of Leroy and Rancoita (2016). For instance, in the Figure below - adapted from Fig. 7.9 at page 509 of Leroy and Rancoita (2016) - it is shown the damage function for protons in silicon for the kinetic energy range 0.1 keV ≤ Ep ≤ 24 GeV: for Jun et al. (2003) with Ed = 21 eV; for Huhtinen (2002) and HGK compilation [Vasilescu and Lindstroem (2000)] with Ed = 20 eV; for Tacconi (2014) - using the screened relativistic NIEL v. 1.5 for the Coulomb contribution - with Ed = 12.9, 21 and 25 eV (data from Appendix A.10 of Leroy and Rancoita (2016)). In the figure, the data are shown interpolated by spline lines. The hadronic contribution to the total NIEL deposition is dominant for incoming kinentic energies of about 20 Mev for protons - see Jun et al (2003), Jun (2017) - and 0.11 GeV/nucleon for alpha-particles - see Jun et al (2004), Jun (2017); a discussion on this topic is avavilable in Section 7.1.1.6 of Leroy and Rancoita (2016).
For compounds, as discussed with respect to both nuclear stopping and electronic stopping powers, similarly NIEL - obtained from nuclear stopping power by means of the partition function - can be determined by means of Bragg's additivity rule. In this way, for a compund the overall NIEL in units of MeV cm2/g is obtained as a weighted sum in which each material contributes proportionally to the fraction of its atomic weight. For instance, in case of a GaAs medium ones obtains (e.g.,, see [Jun et al. (2009)] and Eq. (2.20) at page 15 in [ICRUM (1993)]):
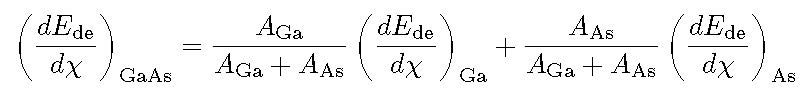
where![]() and AGa [AAs] are the NIEL (in units of MeV cm2/g) and the atomic weight of Gallium [Arsenic], respectively. It has to be remarked that Bragg's additivity rule was established for the energy loss mechanism dominated (by orders of magnitude) by that resulting in ionization energy deposition (e.g., Sect. 2.1.2 of [Leroy and Rancoita (2016)], [ICRUM (1993)], this webpage of Physics Handbook about nuclear stopping power and further discussions about its acuracy at this SRIM webpage). Detailed experimental studies of Bragg's additivity rule started in 1960s.
and AGa [AAs] are the NIEL (in units of MeV cm2/g) and the atomic weight of Gallium [Arsenic], respectively. It has to be remarked that Bragg's additivity rule was established for the energy loss mechanism dominated (by orders of magnitude) by that resulting in ionization energy deposition (e.g., Sect. 2.1.2 of [Leroy and Rancoita (2016)], [ICRUM (1993)], this webpage of Physics Handbook about nuclear stopping power and further discussions about its acuracy at this SRIM webpage). Detailed experimental studies of Bragg's additivity rule started in 1960s.
Finally, the screened relativistic treatments for electrons [Geant4: Class G4eSingleScatteringModel (2014)], protons and ions [Geant4: Class G4IonCoulombScatteringModel (2014)] are inluded in Geant4 simulation code. The complete treatment can be found in Chapers 2, 7 and 8 of [Leroy and Rancoita (2016)].
References
 C. Baur, M. Gervasi, P. Nieminen, S. Pensotti, P.G. Rancoita, M. Tacconi, (2014), NIEL dose dependence for solar cells irradiated with electrons and protons, Proc. of the 14th ICATPP, September 23--27 2013, Villa Olmo, Como, Italy, S. Giani, C. Leroy, L. Price, P.G. Rancoita and R. Ruchti, Editors, World Scientific, Singapore, 698-713; ISBN: 978-981-4603-15-7; http://www.worldscientific.com/doi/pdf/10.1142/9789814603164_0111; http:// arxiv.org/abs/1312.0402
C. Baur, M. Gervasi, P. Nieminen, S. Pensotti, P.G. Rancoita, M. Tacconi, (2014), NIEL dose dependence for solar cells irradiated with electrons and protons, Proc. of the 14th ICATPP, September 23--27 2013, Villa Olmo, Como, Italy, S. Giani, C. Leroy, L. Price, P.G. Rancoita and R. Ruchti, Editors, World Scientific, Singapore, 698-713; ISBN: 978-981-4603-15-7; http://www.worldscientific.com/doi/pdf/10.1142/9789814603164_0111; http:// arxiv.org/abs/1312.0402
M.J. Boschini, C. Consolandi, M. Gervasi, S.Giani, D.Grandi, V. Ivanchenko and P.G. Rancoita, (2010), Geant4-based application development for NIEL calculation in the Space Radiation Environment, Proc. of the 11th ICATPP Conference, October 5-9 2009, Villa Olmo, Como, Italy, World Scientific, Singapore, 698-708, IBSN: 10-981-4307-51-3; http://www.worldscientific.com/doi/pdf/10.1142/9789814307529_0113 .
 M.J. Boschini, C. Consolandi, M. Gervasi, S. Giani, D. Grandi, V. Ivantchenko, S. Pensotti, P.G. Rancoita, M. Tacconi, (2011), Nuclear and Non-Ionizing Energy-Loss for Coulomb Scattered Particle from Low Energy up to relativistic regime in Space Radiation Environment, Proc. of the 12th ICATPP Conference, October 7-8 2010, Villa Olmo, Como, Italy, World Scientific, Singapore, 9-23, IBSN: 978-981-4329-02-6; http://www.worldscientific.com/doi/pdf/10.1142/9789814329033_0002 .
M.J. Boschini, C. Consolandi, M. Gervasi, S. Giani, D. Grandi, V. Ivantchenko, S. Pensotti, P.G. Rancoita, M. Tacconi, (2011), Nuclear and Non-Ionizing Energy-Loss for Coulomb Scattered Particle from Low Energy up to relativistic regime in Space Radiation Environment, Proc. of the 12th ICATPP Conference, October 7-8 2010, Villa Olmo, Como, Italy, World Scientific, Singapore, 9-23, IBSN: 978-981-4329-02-6; http://www.worldscientific.com/doi/pdf/10.1142/9789814329033_0002 . M.J. Boschini, C. Consolandi, M. Gervasi, S. Giani, D. Grandi, V. Ivanchenko, P. Nieminem, S. Pensotti, P.G. Rancoita and M. Tacconi, (2012), Nuclear and Non-Ionizing Energy-Loss of electrons with low and relativistic energies in materials and space environment, Proc. of the 13th ICATPP Conference, October 3-7 2011, Villa Olmo, Como, Italy, World Scientific, Singapore, 961-982, IBSN: 978-981-4405-06-5; http://www.worldscientific.com/doi/pdf/10.1142/9789814405072_0147 .
M.J. Boschini, C. Consolandi, M. Gervasi, S. Giani, D. Grandi, V. Ivanchenko, P. Nieminem, S. Pensotti, P.G. Rancoita and M. Tacconi, (2012), Nuclear and Non-Ionizing Energy-Loss of electrons with low and relativistic energies in materials and space environment, Proc. of the 13th ICATPP Conference, October 3-7 2011, Villa Olmo, Como, Italy, World Scientific, Singapore, 961-982, IBSN: 978-981-4405-06-5; http://www.worldscientific.com/doi/pdf/10.1142/9789814405072_0147 . M.J. Boschini, C. Consolandi, M. Gervasi, S. Giani, D. Grandi, V. Ivanchenko, P. Nieminem, S. Pensotti, P.G. Rancoita, M. Tacconi, (2013), An expression for the Mott cross section of electrons and positrons on nuclei with Z up to 118, Rad. Phys. Chem. 90, 39-66; doi: 10.1016/j.radphyschem.2013.04.020.
M.J. Boschini, C. Consolandi, M. Gervasi, S. Giani, D. Grandi, V. Ivanchenko, P. Nieminem, S. Pensotti, P.G. Rancoita, M. Tacconi, (2013), An expression for the Mott cross section of electrons and positrons on nuclei with Z up to 118, Rad. Phys. Chem. 90, 39-66; doi: 10.1016/j.radphyschem.2013.04.020.
A.V. Butkevick (2002), Nucl. Instr. and Meth. in Phys. Res. A 488, 282-294.
Geant4: Class G4IonCoulombScatteringModel~(2014).
Class Description: Single Scattering Model for protons, alpha and heavy Ions (Ref.~Boschini et al. 2011), Software Reference Manual Source; Code Version: Geant4 10.0 (December 2013) avaliable at the website: http://www-geant4.kek.jp/LXR
See also Sections~6.5--6.5.7 of Physics Reference Manual for version 10.0 available at the website: http://geant4.cern.ch/support/userdocuments.shtml
Geant4: Class G4eSingleScatteringModel (2014). Class Description: single scattering interaction of electrons on nuclei (Ref.~Boschini et al. 2012), Software Reference Manual; Source Code Version: Geant4 10.0 (December 2013) avaliable at the website: http://www-geant4.kek.jp/LXR
See also Sections~6.7--6.8 of Physics Reference Manual for version 10.0 available at the website: http://geant4.cern.ch/support/userdocuments.shtml
H. De Vries,C.W. De Jager and C. De Vries (1987), Atomic Data and Nuclear Data Tables 36, 495.
J.M. Fernandez-Varea et al. (1993), Nucl. Instr. and Meth. in Phys. Res. B 73, 447–473.
Helm, R.H. (1956). Phys. Rev. 104, 1466-1475.
Hofstadter, R. (1957). Ann. Rev. Nucl. Sci. 7, 231.
M. Huhtinen, Nucl. Instr. and Meth. A 491 (2002), 194-215
ICRUM - International Commission on Radiation Units and Measurements - (1993), Stopping Powers and Ranges for Protons and Alpha Particles, ICRU Report 49, Bethesda, MD.
I. Jun (2001), IEEE Trans. on Nucl. Sci. 48, 162-175.
I. Jun et al. (2003), IEEE Trans. on Nucl. Sci 50, 1924-1928.
I. Jun et al (2004), IEEE Trans. on Nucl. Sci 51, 3207-3210
I. Jun et al. (2009), IEEE Trans. on Nucl. Sci. 56, 3229--3235
I.Jun (2017), Private communication regarding hadronic NIEL contribution. See also the web page "Hadronic NIEL contribution for protons and alpha particles".
 C. Leroy and P.G. Rancoita (2011), Principles of Radiation Interaction in Matter and Detection - 3rd Edition -,World Scientific, Singapore, http://www.worldscientific.com/worldscibooks/10.1142/8200, ISBN-978-981-4360-51-7.
C. Leroy and P.G. Rancoita (2011), Principles of Radiation Interaction in Matter and Detection - 3rd Edition -,World Scientific, Singapore, http://www.worldscientific.com/worldscibooks/10.1142/8200, ISBN-978-981-4360-51-7.
 C. Leroy and P.G. Rancoita (2012), Silicon Solid State Devices and Radiation Detection, World Scientific, Singapore, http://www.worldscientific.com/worldscibooks/10.1142/8383, ISBN-978-981-4390-0-0.
C. Leroy and P.G. Rancoita (2012), Silicon Solid State Devices and Radiation Detection, World Scientific, Singapore, http://www.worldscientific.com/worldscibooks/10.1142/8383, ISBN-978-981-4390-0-0.
 C. Leroy and P.G. Rancoita (2016), Principles of Radiation Interaction in Matter and Detection - 4th Edition -, World Scientific. Singapore, https://www.worldscientific.com/worldscibooks/10.1142/9167#t=aboutBook, ISBN-978-981-4603-18-8 (printed); ISBN.978-981-4603-19-5 (ebook); it is also partially accessible via google books.
C. Leroy and P.G. Rancoita (2016), Principles of Radiation Interaction in Matter and Detection - 4th Edition -, World Scientific. Singapore, https://www.worldscientific.com/worldscibooks/10.1142/9167#t=aboutBook, ISBN-978-981-4603-18-8 (printed); ISBN.978-981-4603-19-5 (ebook); it is also partially accessible via google books.
T. Linjian, H. Quing and L. Zhengming (1995), Radiat. Phys. Chem. 45, 235-245.
S.R. Messenger et al. (2004), IEEE Trans. on Nucl. Sci. 51, 2846-2850.
N.F. Mott (1929), Proc. Roy. Soc. A 124, 425-442; A 135 (1932), 429-458.
Vasilescu and Lindstroem (2000), compilation previously available on line including neutron damage functions and protons from a private communication of Huhtinen and Aarnio (1993) on the energy range 15MeV -- 9.0 GeV.