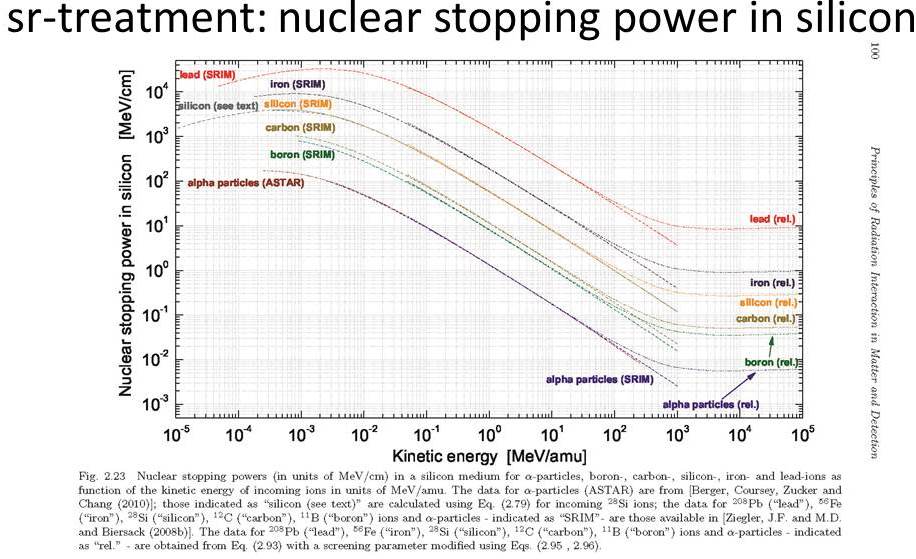
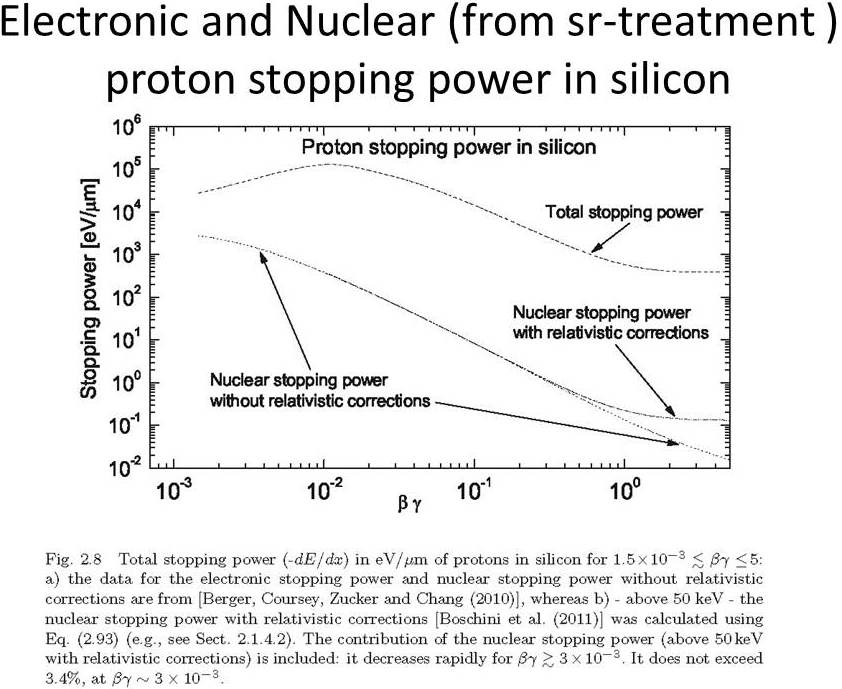
The above figure are from C. Leroy and P.G. Rancoita (2011), Principles of Radiation Interaction in Matter and Detection - 3rd Edition -, World Scientific, Singapore, ISBN-978-981-4360-51-7; http://www.worldscientific.com/worldscibooks/10.1142/8200.
The reader may se also C. Leroy and P.G. Rancoita (2016), Principles of Radiation Interaction in Matter and Detection - 4th Edition -, World Scientific. Singapore, https://www.worldscientific.com/worldscibooks/10.1142/9167#t=aboutBook ISBN-978-981-4603-18-8 (printed); ISBN.978-981-4603-19-5 (ebook).
Using the expression describing the screened Coulomb nucleus–nucleus scattering (e.g., Sect. 2.2.2 of [Leroy and Rancoita (2016)]):
![( ) 2 [ ( ) ]
dE- ( 2)2 --E---- -1-
- dx = 2πnA zZe p2M c4 ln As - 1 ,
nucl](/images/images_handbook/Coulombnuclearstoppingp0x.png) | (1) |
above 50 keV/nucleon (e.g., see here) the nuclear stopping power - in MeV cm-1 - is obtained as:
with nA the number of nuclei (atoms) per unit of volume and, finally, the negative sign indicates that the energy is lost by the incoming particle (thus, achieved by recoil targets). For energies higher than a few tens of keVs, because As ≪ 1, Eq. (3) can be re-written as
![( ) [ ( ) ]
dE ( 2)2 E2 1
- --- = 2πnA zZe -2---4- ln --- - 1 .
dx nucl p M c As](/images/images_handbook/Coulombnuclearstoppingp2x.png) | (4) |
It has to be noted that, as the incoming momentum increases to a value for which p ≃ E, the set of terms - in front of those included in brackets - decreases and approaches a constant; while the term ln 1∕As increases as ln(p) for E ≫ mc2,Mc2. Thus, a slight increase of the nuclear stopping power with energy is expected because of the decrease of the screening parameter with energy.
For energies lower than 50-200 keV/nucleon, the scattering of protons and screened nuclei can be treated using the 4-terms analytical approximation of the ZBL cross section derived by Messenger et al. (2004) [see Eqs. (1--3, 15) and also references therein]. The non-relativistic approach - based on the universal screening potential - of [Ziegler, Biersack and Littmark (1985)] was also used in [ICRU Report 49 (1993)] to calculate nuclear stopping powers - currently available on the web (e.g., see [Berger, Coursey, Zucker and Chang (2005)]) - due to protons and α-particles in materials. In Fig. 1, the variation (in percentage) of nuclear stopping powers - calculated with Eq. (3) - with respect to ICRU tabulated values [3] is shown as a function of the kinetic energy per nucleon (in MeV/nucleon) - for energies from 50 keV/nucleon up to 100 MeV/nucleon - for protons and α-particles traversing amorphous carbon, silicon, germanium and lead media. The stopping powers for protons (α-particles) from Eq. (3) are less than ≈ 5% larger than those reported by ICRU (1993) from 50 keV/nucleon up to ≈ 32 MeV (31 MeV/nucleon) - the upper energy corresponds to ϵr,U ≈ 6.2 × 104 (4.3 × 104) for protons in an amorphous carbon (α-particles in a silicon) medium -. At larger energies the stopping powers from Eq. (3) differ from those from ICRU - as expected - due to the complete relativistic treatment of the present approach.
The simple screening parameter used so far - derived by [Molière (1947, 1948)] - can be modified by means of a practical correction, i.e.,
![( )2 [ ( )2 ]
A ′= ---ℏ---- 1.13 + 3.76 × ℂ αzZ-- ,
s 2 p′in aI βr](/images/images_handbook/Coulombnuclearstoppingp5x.png) | (5) |
to achieve a better agreement with low energy calculations of Ziegler, Biersack and Littmark (1985). For instance, for protons, α-particles and heavier ions, with
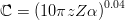 | (6) |
the stopping powers obtained from Eq. (3) - in which As′ replaces As - differ from the values of SRIM (2008) by less than ≈ 3.5 (2.6) % for α-particles (lead ions) in silicon down to about 50 keV/nucleon. With respect to the tabulated values of ICRU (1993), the agreement for α-particles is usually better than 2% at low energy down to 50 keV/nucleon (Fig. 2) - a 1% agreement is achieved at about 50 keV/nucleon in case of a carbon (or silicon) medium. At very high energy, the stopping power is slightly affected when As′ replaces As: for example, a) in silicon at ultra high-energies [Boschini et al. (2011)] the nuclear stopping power of α-particles (lead-ions) is decreased by about 0.03 (0.71) % and b) in lead it is decreased by about 0.4 (1.0) %.
It has to be remarked that the nuclear stopping power for screened Coulomb elastic scattering up to relativistic energies is currently included in the Geant4 code ([Agostinelli et al. (2003), Geant4: Class G4IonCoulombScatteringModel (2015)]).
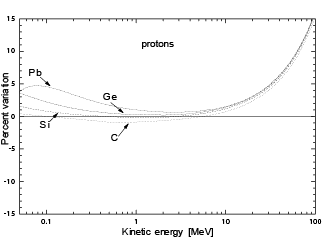
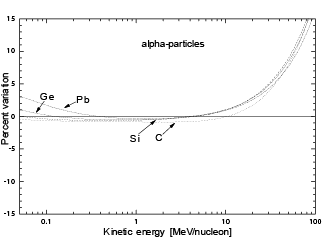
Figure 1:
Variation (in percentage) of nuclear stopping powers - calculated
with Eq. (3) for energies from 50 keV/nucleon up to 100 MeV/nucleon - with
respect to ICRU tabulated values [ICRU Report 49 (1993)] as a function
of the kinetic energy in MeV/nucleon, for protons (top) and α-particles
(bottom) traversing amorphous carbon, silicon, germanium and lead media
(from [Boschini et al. (2011)]).
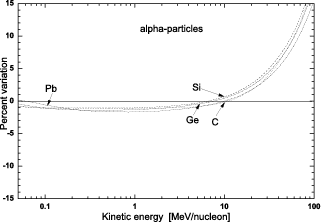
Figure 2:
Variation (in percentage) of nuclear stopping powers - calculated
with Eq. (3) with the expressions (5, 6) for the screening parameter - with
respect to ICRU tabulated values [ICRU Report 49 (1993)] as a function
of the kinetic energy in MeV/nucleon, for α-particles traversing amorphous
carbon, silicon, germanium and lead media for energies from 50 keV/nucleon
up to 100 MeV/nucleon (from [Boschini et al. (2011)]).
References


Variation (in percentage) of nuclear stopping powers - calculated with Eq. (3) for energies from 50 keV/nucleon up to 100 MeV/nucleon - with respect to ICRU tabulated values [ICRU Report 49 (1993)] as a function of the kinetic energy in MeV/nucleon, for protons (top) and α-particles (bottom) traversing amorphous carbon, silicon, germanium and lead media (from [Boschini et al. (2011)]).

Variation (in percentage) of nuclear stopping powers - calculated with Eq. (3) with the expressions (5, 6) for the screening parameter - with respect to ICRU tabulated values [ICRU Report 49 (1993)] as a function of the kinetic energy in MeV/nucleon, for α-particles traversing amorphous carbon, silicon, germanium and lead media for energies from 50 keV/nucleon up to 100 MeV/nucleon (from [Boschini et al. (2011)]).
[Agostinelli et al. (2003)] S. Agostinelli et al. (2003), Geant4 a simulation toolkit, Nucl. Instr. and Meth. in Phys. Res. A 506, 250–303.
[Berger, Coursey, Zucker and Chang (2005)] M.J. Berger, J.S. Coursey, M.A. Zucker and J. Chang, data from ESTAR, PSTAR and ASTAR (version 1.2.3, August 2005); available on the web site (2010): http://physics.nist.gov/Star; originally published as: M.J. Berger, NISTIR 4999, NIST, Gaithersburg, MD (1993).
[Boschini et al. (2011)] M.J. Boschini, C. Consolandi, M. Gervasi, S. Giani, D. Grandi, V. Ivantchenko, S. Pensotti, P.G. Rancoita, M. Tacconi, Nuclear and Non-Ionizing Energy-Loss for Coulomb Scattered Particle from Low Energy up to relativistic regime in Space Radiation Environment, Proc. of the 12th ICATPP Conference, October 7-8 2010, Villa Olmo, Como, Italy, World Scientific, Singapore (2011), 9-23, IBSN: 978-981-4329-02-6; http://www.worldscientific.com/doi/pdf/10.1142/9789814329033_0002 or http://arxiv.org/pdf/1011.4822v7.pdf.
[Geant4: Class G4IonCoulombScatteringModel (2015)] Geant4: Class G4IonCoulombScatteringModel (2015), Class Description: Single Scattering Model for protons, alpha and heavy Ions ([Boschini et al. (2011)]), Software Reference Manual Source Code Version: Geant4 10.n avaliable at the website http://www-geant4.kek.jp/LXR. See also Sections 6.5–6.5.7 of Physics Reference Manual for version 10.n available at the website: http://geant4.cern.ch/support/userdocuments.shtml.
[ICRU Report 49 (1993)] ICRU, ICRU Report 49, Stopping Powers and Ranges for Protons and Alpha Particles (1993).
[Leroy and Rancoita (2016)] C. Leroy and P.G. Rancoita (2016), Principles of Radiation Interaction in Matter and Detection - 4th Edition -, World Scientific. Singapore, ISBN-978-981-4603-18-8 (printed); ISBN.978-981-4603-19-5 (ebook); https://www.worldscientific.com/worldscibooks/10.1142/9167#t=aboutBook; it is also partially accessible via google books.
[Messenger et al. (2004] Messenger et al., IEEE Trans. on Nucl. 51 (2004), 2846–2850.
[Molière (1947, 1948)] von G. Molière, Z. Naturforsh. A2 (1947), 133–145; A3 (1948), 78.
[SRIM (2008)] SRIM: J.F. Ziegler, M.D. Ziegler and J.P. Biersack, The Stopping and Range of Ions in Matter, version 2008.03 (2008), available at: http://www.srim.org/
[Ziegler, Biersack and Littmark (1985)] J.F. Ziegler, J.P. Biersack and U. Littmark, The Stopping Range of Ions in Solids, Vol. 1, Pergamon Press (New York) 1985.


![( ) ∫ Tmax W M
- dE- = n dσ----(T)-T dT (2)
dx nucl A 0 dT
2 ∫ Tmax
= 2nA π (zZe2 )2--E---- ------T-------dT
p2M c4 0 [AsTmax + T]2
( ) E2 [ A (A + 1)]
= 2nA π zZe2 2------- ----s--- 1 + ln --s---- (3)
p2M c4 As + 1 As](/images/images_handbook/Coulombnuclearstoppingp1x.png)