Fast neutrons, as well as other types of particles, produce defects mainly by displacing silicon atoms from their lattice positions to interstitial locations, i.e., generating vacancy-interstitial pair, the so-called Frenkel pairs. Neutrons with sufficient large energies (i.e. fast neutrons) can cause the displacement of a silicon or any other atom inside the lattice, referred to as primary displacement, from its location. The displaced arom can, in turn, generate secondary displacements, following a cascading effect. In literature (see for instance[Namenson, Wolicki and Messenger (1982), Ougouag et al. (1990), ASTM E722-09 (2009), ASTM E722-14 (2014)]), the damage effect due to displacements induced by neutrons is expressed by the damage function D(E) in units of MeV cm2, also called the displacement kerma function, whose value, for instance, in Si at 1 MeV is the ASTM standard [ASTM E722-09 (2009), ASTM E722-14 (2014)] D(1 MeV)≈95 MeV mb. The damage function accounts for both the cross section for displacing silicon atoms and the energy released in creating displacements. It is given by:
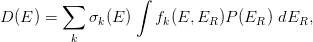 | (1) |
where E is the incoming neutron energy, σk(E) is the cross section for the kth reaction in which fk(E,ER) is the probability that a recoil energy ER is generated and, finally, P(ER) is the partition energy, i.e., the part of the recoil energy deposited in displacements calculated, for instance, in the framework of the Lindhard screened potential scattering theory, based on the Thomas-Fermi model and further developments[Lindhard, Nielsen, Scharff and Thomsen (1963), Coulter and Parkin (1977), Coulter and Parkin (1979), Coulter and Parkin (1980)]. The damage function is given in literature (e.g., see [Ougouag et al. (1990)] and references therein). The damage functions were obtained in [ASTM E722-09 (2009), ASTM E722-14 (2014)] for Ed = 25 and 20.5 eV, respectively, in Si and 10 eV in GaAs, where Ed is the is the so-called displacement threshold energy.
The energy density Edis is the energy per cm3 deposited through atomic displacements by neutrons, which are characterized by the spectral fluence ϕ(E) in n/cm2 MeV, and is given by:
![∫
Edis = N D (E ) ϕ(E ) dE [MeV cm -3]
Emin](/images/images_handbook/1MeVneutron1x.png) | (2) |
where N is the number of atoms per cm3 in the bulk silicon and E min is the lowest neutron kinetic energy for displacement. Edis, as computed by means of Eq. (2), is the Non Ionizing Energy Loss (NIEL in units of MeV/cm) deposited by the neutrons per cm2 of the absorber (e.g., treatment in Chapter 4 of [Leroy and Rancoita (2011], Chapter 7 of [Leroy and Rancoita (2016)]: as long as Emin is ≲ 10 keV, Edis varies slightly. In the case of the Triga reactor RC:1 neutron spectrum, the Edis value varies by no more than 0.5 % for Emin values in the energy range up to 10 keV (e.g., see [Consolandi et al. (2006), Leroy and Rancoita (2007)] and references therein).
In the current sr-niel calculator (e.g., see [sr-niel.org (2016)]) the NIEL and NIEL doses are determined by means of the damage functions from [ASTM E722-09 (2009), ASTM E722-14 (2014)].
The displacement damages induced by neutrons can be normalized to displacement damages induced by 1 MeV neutrons by means of the hardness parameter (κ) also termed hardness factor. For fission neutrons with spectral fluence ϕ(E), the 1 MeV equivalent neutron fluence is given by:
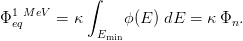 | (3) |
Φeq1 MeV is the fluence of 1 MeV neutron needed for generating the same amount of displacement damage compared to the fission fluence Φn.
From Eqs. (2, 3), we can derive the hardness parameter κ as:
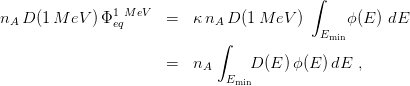
![[∫ ] ( ∫ ) -1
κ = ---D-(E-)-- ϕ(E) dE ϕ(E ) dE
EminD (1 M eV ) Emin](/images/images_handbook/1MeVneutron4x.png) | (4) |
and, conversely,
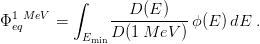 | (5) |
References
[ASTM E722-09 (2009)] ASTM E722–09 (2009).
[ASTM E722-14 (2014)] ASTM-722–14 (2014).
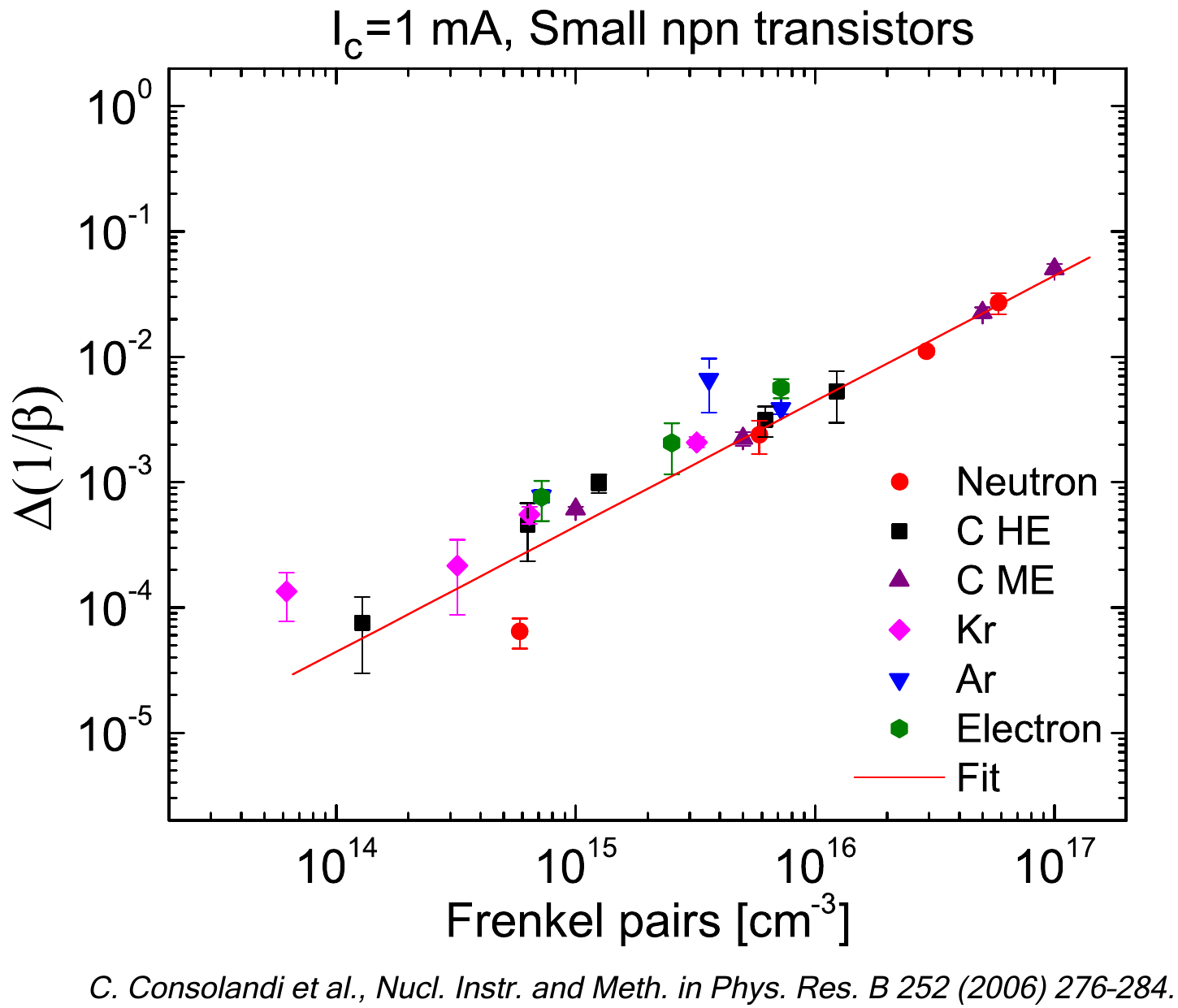
[Consolandi et al. (2006)] C. Consolandi et al. (2006), Systematic Investigation of Monolithic Bipolar Transistors Irradiated with Neutrons, Heavy Ions and Electrons for Space Applications, Nucl. Instr. and Meth. in Phys. Res. B 252 (2006), 276, doi:10.1016/j.nimb.2006.08.018; http://www.sciencedirect.com/science/article/pii/S0168583X0600913X.
[Coulter and Parkin (1977)] C. A. Coulter and D. M. Parkin, Trans. Am. Nucl. Soc. 27 (1977), 300.
[Coulter and Parkin (1979)] C. A. Coulter and D. M. Parkin, Jou. Nucl. Mat. 85&86 (1979), 611.
[Coulter and Parkin (1980)] C. A. Coulter and D. M. Parkin, Jou. Nucl. Mat. 88 (1980), 249.
[Leroy and Rancoita (2007)] C. Leroy and P.G. Rancoita (2007), Particle Interaction and Displacement Damage in Silicon Devices operated in Radiation Environments Reports on Progress in Physics 70, 493-625, doi:10.1088/0034-4885/70/4/R0; http://iopscience.iop.org/0034-4885/70/4/R01/.
[Leroy and Rancoita (2011)] C. Leroy and P.G. Rancoita (2011), Principles of Radiation Interaction in Matter and Detection - 3rd Edition -, World Scientific, Singapore, ISBN-978-981-4360-51-7; http://www.worldscientific.com/worldscibooks/10.1142/8200.
[Leroy and Rancoita (2016)] C. Leroy and P.G. Rancoita (2016), Principles of Radiation Interaction in Matter and Detection - 4th Edition -, World Scientific. Singapore, ISBN-978-981-4603-18-8 (printed); ISBN.978-981-4603-19-5 (ebook); https://www.worldscientific.com/worldscibooks/10.1142/9167#t=aboutBook; it is also partially accessible via google books.
[Lindhard, Nielsen, Scharff and Thomsen (1963)] J. Lindhard, V. Nielsen, M. Scharff and P. V. Thomsen, Danske Vidensk. Selsk. Mat.-Fys. Medd. 33 vol. 10 (1963), 10
[Namenson, Wolicki and Messenger (1982)] A. I. Namenson, E. A. Wolicki and G.C. Messenger, IEEE Trans on Nucl. Sci. 29 (1982) 1018.
[Ougouag et al. (1990)] A. M. Ougouag et al., IEEE Trans on Nucl. Sci. 37 (1990) 2219.