Probability of Energetic Recoil Nuclei and Nuclear Coulomb Cross Section for Elements and Compounds

Energetic Recoil Nuclei generated via Elastic Coulomb Scattering of Electrons, Protons, Ligh- and Heavy-Ions in a Medium

The Coulomb (elastic) cross section for the scattering of a charged particle (electrons, protons, light- and heavy ions) is obtained from:

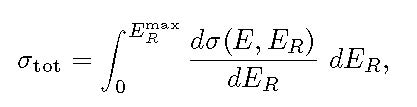
where E is the kinetic energy of the incoming particle, E_R and E_R^max are the kinetic energy and the maximum energy transferred to the recoil nucleus, respectively; finally is the differential cross section for elastic Coulomb scattering of electrons or protons or ions on nuclei. The cross section for the occurrence of a recoil nucleus with kinetic energy larger than  E_ener  is given by:

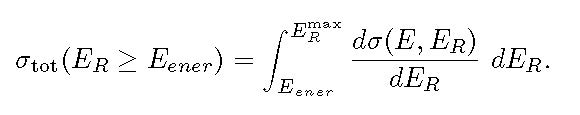
Furthermore, the probability that  - traversing a medium of thickness x – an energetic recoil nucleus (with kinetic energy equal or larger than E_ener ) is obtained from:

where

is the number of atoms per cm³ in the absorber,  ρ_A and A are the density and atomic weight of the medium, respectively; N is the Avogadro constant.
In the framework of the screened relativistic treatment for nuclear elastic scattering, the values of the nuclear mass stopping power in units of MeV cm²/g for electrons are obtained using the Mott differential cross section [Mott (1929)] of electrons on nuclei calculated from the practical expression discussed in [Boschini et al. (2013)] (see also [Linjian et al. (1995)]) and accounting for the effects due to both screened nuclear potentials and form factors discussed in [Boschini et al. (2012)] and Sects. 1.3.1-1.3.3 of [Leroy and Rancoita (2012)]  (see also references therein). Hereafter, (i.e., see Chapter 2 in [Leroy and Rancoita (2016)]) is reported the discussion about the currently implemented form factors in this calculation of the nuclear stopping power and screened relativistic NIEL.

The Coulomb nuclear (elastic) cross sections for protons and nuclei above 50 keV/nucleon is obtained using the elastic cross section derived from treatment of the nucleus-nucleus screened Coulomb scattering discussed in [Boschini et al. (2011)] and Sect. 2.1.4.2 in [Leroy and Rancoita (2011)] (see also [Fernandez-Varea et al. (1993),Butkevick (2002), Boschini et al. (2010)]). That treatment allows one to deal with a scattering occurring up to relativistic energies.
For energies lower than 50-200 keV/nucleon, the scattering of protons and screened nuclei can be treated using the 4-terms analytical approximation of the ZBL cross section derived by Messenger et al. (2004) [see Eqs. (1--3, 15) and also references therein].
For a compound, the probability Prob_Comp(E_R > E_ener) divided by the compound density ρ_comp can be determined by means of Bragg's additivity rule, i.e., the overall value is obtained as a weighted sum in which each material contributes proportionally to the fraction of its atomic weight. For instance, in case of a GaAs medium ones obtains:

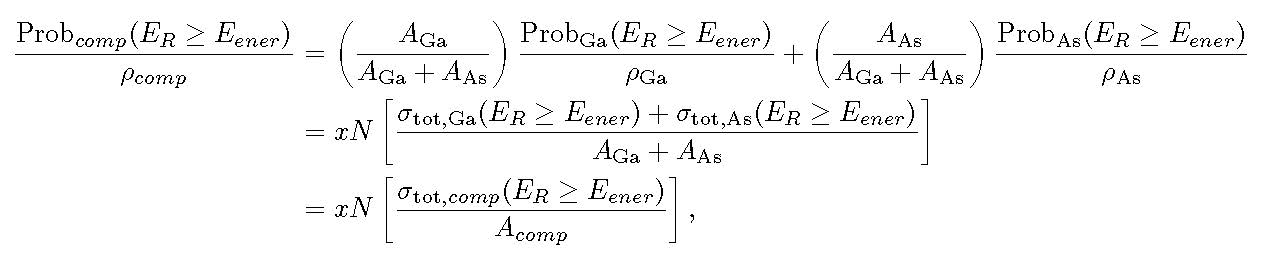
where  A_Ga [A_As], ρ_Ga [ρ_As], Prob_Ga(E_R ≥ E_ener) [Prob_As(E_R ≥ E_ener)], σ_tot,Ga(E_R ≥ E_ener) [σ_tot,As(E_R ≥ E_ener)] are the atomic weight, density, probability of interaction, cross section of Gallium [Arsenic], respectively; finally

and

are the GaAs compound cross section and atomic weight, respectively. Finally, the probability R(E_ener) per g/cm² is given by (Chapter 2 of [Leroy and Rancoita (2015)]):

R(E_ener)=

It has be remarked that the screened relativistic treatments for electrons [Geant4: Class G4eSingleScatteringModel (2014)], protons and ions [Geant4: Class G4IonCoulombScatteringModel (2014)] are inluded in Geant4 simulation code. The complete treatment can be found in Chapters 2, 7 and 8 of [Leroy and Rancoita (2015)].
 

References

M.J. Boschini, C. Consolandi, M. Gervasi, S.Giani, D.Grandi, V. Ivanchenko and P.G. Rancoita, (2010), Geant4-based application development for NIEL calculation in the Space Radiation Environment, Proc. of the 11th ICATPP Conference, October 5-9 2009, Villa Olmo, Como, Italy, World Scientific, Singapore, 698-708, IBSN: 10-981-4307-51-3;http://www.worldscientific.com/doi/pdf/10.1142/9789814307529_0113 .
 
M.J. Boschini, C. Consolandi, M. Gervasi, S. Giani, D. Grandi, V. Ivantchenko, S. Pensotti, P.G. Rancoita, M. Tacconi, (2011), Nuclear and Non-Ionizing Energy-Loss for Coulomb Scattered Particle from Low Energy up to relativistic regime in Space Radiation Environment, Proc. of the 12th ICATPP Conference, October 7-8 2010, Villa Olmo, Como, Italy, World Scientific, Singapore, 9-23, IBSN: 978-981-4329-02-6; http://www.worldscientific.com/doi/pdf/10.1142/9789814329033_0002 .

  
M.J. Boschini, C. Consolandi, M. Gervasi, S. Giani, D. Grandi, V. Ivanchenko, P. Nieminem, S. Pensotti, P.G. Rancoita and M. Tacconi, (2012), Nuclear and Non-Ionizing Energy-Loss of electrons with low and relativistic energies in materials and space environment, Proc. of the 13th ICATPP Conference, October 3-7 2011, Villa Olmo, Como, Italy, World Scientific, Singapore, 961-982, IBSN: 978-981-4405-06-5;http://www.worldscientific.com/doi/pdf/10.1142/9789814405072_0147 .

 
M.J. Boschini, C. Consolandi, M. Gervasi, S. Giani, D. Grandi, V. Ivanchenko, P. Nieminem, S. Pensotti, P.G. Rancoita, M. Tacconi, (2013), An expression for the Mott cross section of electrons and positrons on nuclei with Z up to 118, Rad. Phys. Chem. 90, 39-66; doi: 10.1016/j.radphyschem.2013.04.020.

 
A.V. Butkevick (2002), Nucl. Instr. and Meth. in Phys. Res. A 488, 282-294.
 
H. De Vries,C.W. De Jager and C. De Vries (1987), Atomic Data and Nuclear Data Tables 36, 495.
 
Geant4: Class G4IonCoulombScatteringModel~(2014). Class Description: Single Scattering Model for protons, alpha and heavy Ions (Ref.~Boschini et al. 2011), Software Reference Manual, Source Code Version: Geant4 10.0 (December 2013) avaliable at the website
http://www-geant4.kek.jp/LXR
See also Sections~6.5--6.5.7 of Physics Reference Manual for version 10.0 available at the website:
http://geant4.cern.ch/support/userdocuments.shtml
 
Geant4: Class G4eSingleScatteringModel (2014). Class Description: single scattering interaction of  electrons on nuclei (Ref.~Boschini et al. 2012), Software Reference Manual. Source Code Version: Geant4 10.0 (December 2013) avaliable at the website
http://www-geant4.kek.jp/LXR
See also Sections~6.7--6.8 of Physics Reference Manual for version 10.0 available at the website:
http://geant4.cern.ch/support/userdocuments.shtml
 
ICRUM - International Commission on Radiation Units and Measurements - (1993), Stopping Powers and Ranges for Protons and Alpha Particles, ICRU Report 49, Bethesda, MD.
 
I. Jun et al. (2003), IEEE Trans. on Nucl. Sci 50, 1924-1928.
 

C. Leroy and P.G. Rancoita (2011),  Principles of Radiation Interaction in Matter and Detection - 3rd Edition -,World Scientific, Singapore, ISBN-978-981-4360-51-7; http://www.worldscientific.com/worldscibooks/10.1142/8200 .

C. Leroy and P.G. Rancoita (2012), Silicon Solid State Devices and Radiation Detection, World Scientific, Singapore, ISBN-978-981-4390-0-0; http://www.worldscientific.com/worldscibooks/10.1142/8383 .

C. Leroy and P.G. Rancoita (2016), Principles of Radiation Interaction in Matter and Detection - 4th Edition -, World Scientific. Singapore, ISBN-978-981-4603-18-8 (printed); ISBN.978-981-4603-19-5 (ebook). https://www.worldscientific.com/worldscibooks/10.1142/9167#t=aboutBook; it is also partially accessible via google books.

 
T. Linjian, H. Quing and L. Zhengming (1995), Radiat. Phys. Chem. 45, 235-245.
 
S.R. Messenger et al. (2004), IEEE Trans. on Nucl. Sci. 51, 2846-2850.
 
N.F. Mott (1929), Proc. Roy. Soc. A 124, 425-442; A 135 (1932), 429-458.
 
J.M. Fernandez-Varea et al. (1993), Nucl. Instr. and Meth. in Phys. Res. B 73, 447–473.

Helm, R.H. (1956). Phys. Rev. 104, 1466-1475.

Hofstadter, R. (1957). Ann. Rev. Nucl. Sci. 7, 231.

E. Zeitler and A. Olsen, Phys. Rev. 136 (1956), A1546-A1552.

J.M. Fernandez-Varea, R. Mayol and F. Salvat, Nucl. Instr. and Meth. in Phys. Res. B82, (1993) 39-45

B.Hahn et al. Phys. Rev. 101 (1956) 1131