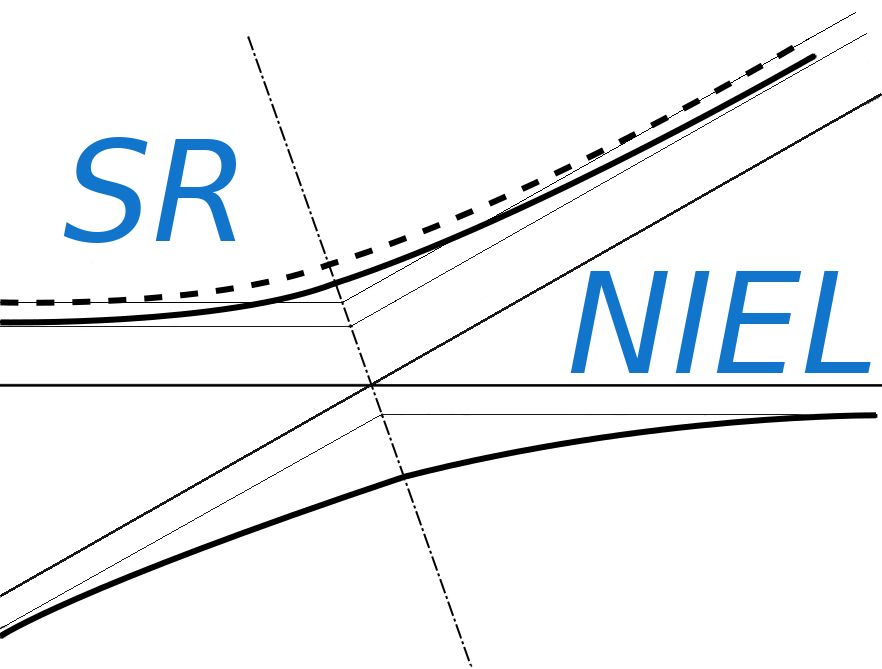
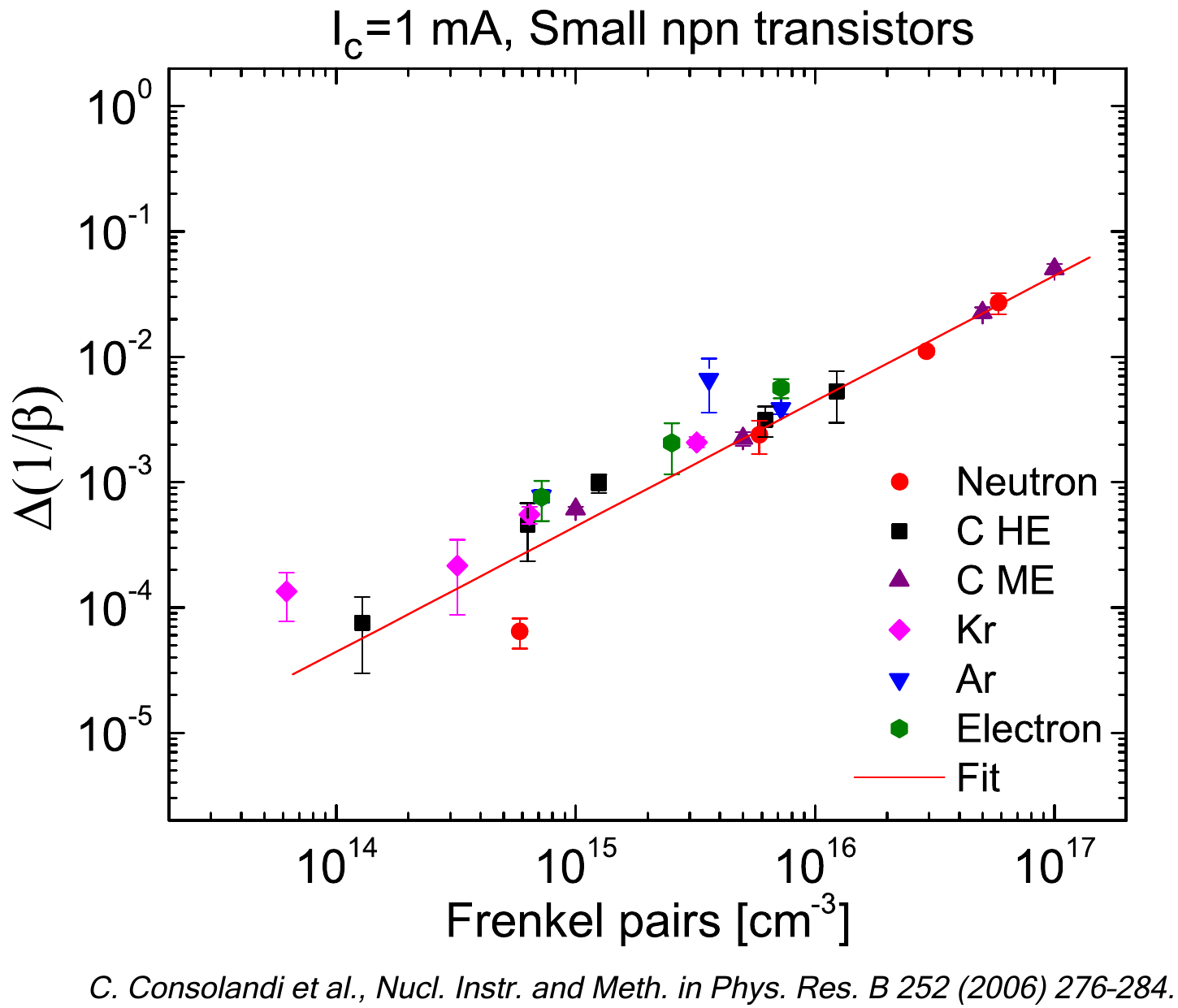
As treated in Section 8.3.2 of [Leroy and Rancoita (2016)], the kinetic energies (E) of reactor fission neutrons do not exceed ≈ 15 MeV. However, the available fission spectra differ for the energy distribution of both thermal and fast neutrons and are characterized by a neutron spectral-fluence ϕ(E) in n/(cm2 MeV) obtained as
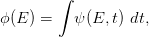 | (1) |
where ψ(E,t) is the neutron spectral-flux in n/(s cm2 MeV), and by a neutron fluence
![∫
Φn = ϕ (E ) dE [n/cm2 ],
Emin](/images/images_handbook/neutronspectralfluence1x.png) | (2) |
where Emin is the minimum neutron kinetic-energy (typically about 10 keV) to induce radiation damage by atomic displacements (see for instance Section 5.9 in [Messenger and Ash (1992)]). Thus, Φn accounts for the neutron fluence1 related to radiation-induced damages, i.e., above 10 keV in n–silicon interactions, the energy released for displacement damages is no longer negligible.
The displacement damages induced by neutrons can be normalized to displacement damages induced by 1 MeV neutrons by means of the hardness parameter (κ) also termed hardness factor (for a further discussion, see for instance [Namenson, Wolicki and Messenger (1982), Kelly, Luera, Posey and Williams (1988), Vasilescu (1997)]). For fission neutrons with spectral fluence ϕ(E), the 1 MeV equivalent neutron fluence is given by:
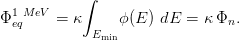 | (3) |
Φeq1 MeV is the fluence of 1 MeV neutron needed for generating the same amount of displacement damage compared to the fission fluence Φn.
References
[Kelly, Luera, Posey and Williams (1988)] J.G. Kelly, T.F. Luera, L.D. Posey and J.G. Williams (1988). IEEE Trans. Nucl. Sci. 35, 1242.
[Leroy and Rancoita (2016)] C. Leroy and P.G. Rancoita (2016), Principles of Radiation Interaction in Matter and Detection - 4th Edition -, World Scientific. Singapore, ISBN-978-981-4603-18-8 (printed); ISBN.978-981-4603-19-5 (ebook); https://www.worldscientific.com/worldscibooks/10.1142/9167#t=aboutBook; it is also partially accessible via google books.
[Messenger and Ash (1992)] G.C. Messenger and M.S. Ash (1992). The Effects of Radiation on Electronic Systems - 2nd Edition -, Van Nostrand Reinhold Company, New York; 1st Edition (1986).
[Namenson, Wolicki and Messenger (1982)] A. I. Namenson, E. A. Wolicki and G.C. Messenger, IEEE Trans on Nucl. Sci. 29 (1982) 1018.
[Vasilescu (1997)] A. Vasilescu, (1997). The NIEL scaling hypothesis applied to neutron spectra of irradiation facilities in the ATLAS and CMS SCT, ROSE/TN/97-2. See also: A. Vasilescu and G. Lindstroem (2000). Notes on the fluence normalization based on the NIEL scaling hypothesis ROSE/TN/2000-02
1The total neutron fluence can be computed with Emin = 0.