The occurance probability of events due to large energy depositions in a device - like those commonly referred to as single event effects (SEE) – is usually expressed by means of the cross section as a function of mass electronic stopping power - or mass restricted energy loss - of the device material (e.g., see Sects. 11.4-11.4.9 of [Leroy and Rancoita (2016)] and references therein).
As discussed in this webpage, one can re-express that device cross section as a function of the energy of incoming particles. In this way, the overall events occurrence can be estimated using the entire range of particle spectral fluence. In fact, nowadays the spectral fluences of low- and high-Z cosmic rays were observed up to very high energies (e.g., see here).
The following link allows one to access to the Probability of events occurrence due to a large energy deposition in devices calculator for protons and ions:
How to use this calculators for probability of events occurrence due to a large energy deposition in devices
This tool calculates the Probability of events occurrence due to a large energy deposition in devices for a spectral fluence incident on a material.
The input parameters and options for the tool are described below. When the input form has been completed, pressing the "CALCULATE" button will start the calculation and open the "Results" page (allow for pop-up in your browser settings). The result page will be also linked at the bottom of the calculator page.
Input Parameters:
- Device material
- SEE Cross section (Weibull function parameters)
- Energy Loss Type
- Incident particle
- Spectral fluence
Currently, as an example, the default parameters for the Weibull function are those for the device treated in this webpage.
Device Material
In the section "Device Material Selection" it is possible to specify an User Defined device material or a predefined Compound. User can also select the device as a gas, this is allowed only for single element and natural gas target (H, He, N, O, F, Ne, Cl, Ar, Kr, Xe, Rn).
The stopping power in target gases is usually higher than that in an equivalent solid target. The Gas/ Solid correction disappears for higher velocity ions with energies above 2 MeV/amu. But at lower velocities the effect can be quite large - almost a 2 times change in stopping bacause of the Phase effect near the Bohr velocity, 25 keV/amu.
in the User Defined section individual elements can be selected as well as the composition of the device material choosing the number of elements in the compound. The required parameters for each element are:
- Atomic number (Z)/Chemical symbol
- Stoichiometric index or element fraction
Electronic Stopping Power for User Defined Compounds
Electronic Stopping Power for User Defined Compounds can be determined by means of Bragg's additivity rule, i.e., the overall Electronic Stopping Power in units of MeV cm2/g (i.e., the mass electronic stopping power) is obtained as a weighted sum in which each material contributes proportionally to the fraction of its atomic weight. For instance, in case of a GaAs medium ones obtains (e.g., Eq. (2.20) at page 15 in [ICRUM (1993)]):
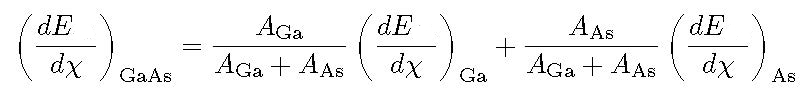
where ![]() and AGa [AAs] are the Electronic Stopping Power (in units of MeV cm2/g) and the atomic weight of Gallium [Arsenic], respectively.
and AGa [AAs] are the Electronic Stopping Power (in units of MeV cm2/g) and the atomic weight of Gallium [Arsenic], respectively.
For few compounds belonging to the ICRU list the parameters employed for the energy loss formula (including those for the densiity effect) are reported in Table II of Sternheimer et al. (1984).
Further discussion can be found in the help of the SR-framewrok electronic stopping (see also results page).
SEE Cross section
This section define parameters that are included in the Weibull function:
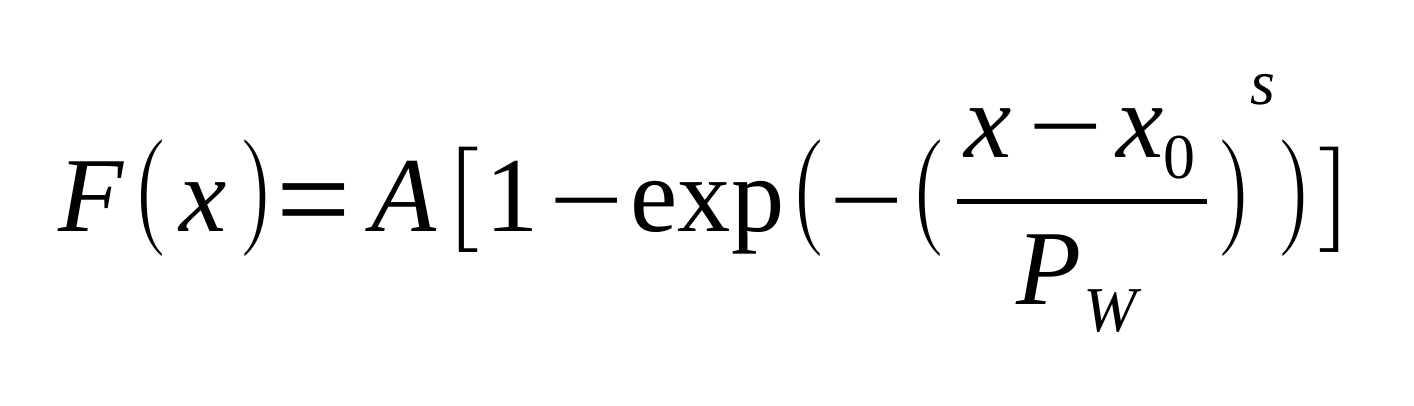
where x is the stopping power (or the restricted energy loss) in MeV cm2 mg-1, A is the saturation cross section, x0 is the stopping power (or LET) threshold parameter, PW is the width parameter and s is a dimensionless exponent.
Energy Loss type
The user can select 3 different energy loss types:
- SRIM Electronic Stopping Power
- SR-Framework Electronic Stopping
- SR-Framework Restricted Energy Loss
When restricted energy loss is selected, the Effective detectable energy W0 can be modified: the current default value is 100 keV.
For the conversion of the cross section as a function of the incoming particle energy, the input cross section is assumed to be provided as a function of the corresponding type of the selected energy loss (i.e., SRIM Electronic stopping power, SR-Framework Electronic stopping, SR-Framework Restricted energy loss). One has to remark that SRIM Electronic stopping power and SR-Framework Stopping power agree within 5% (or better) up to the maximum energy obtained from SRIM Module.exe (i.e., 5 GeV/amu), see discussion here.
As discussed at page 70 of [Leroy and Rancoita (2016)] for all incoming particle energy for which the maximum transferred energy W (see Eq. (1.29) of [Leroy and Rancoita (2016)]) is lower than or equal to W0 there is no difference in between the SR-Framework electronic stopping power and the restricted energy loss (see Figure 1).
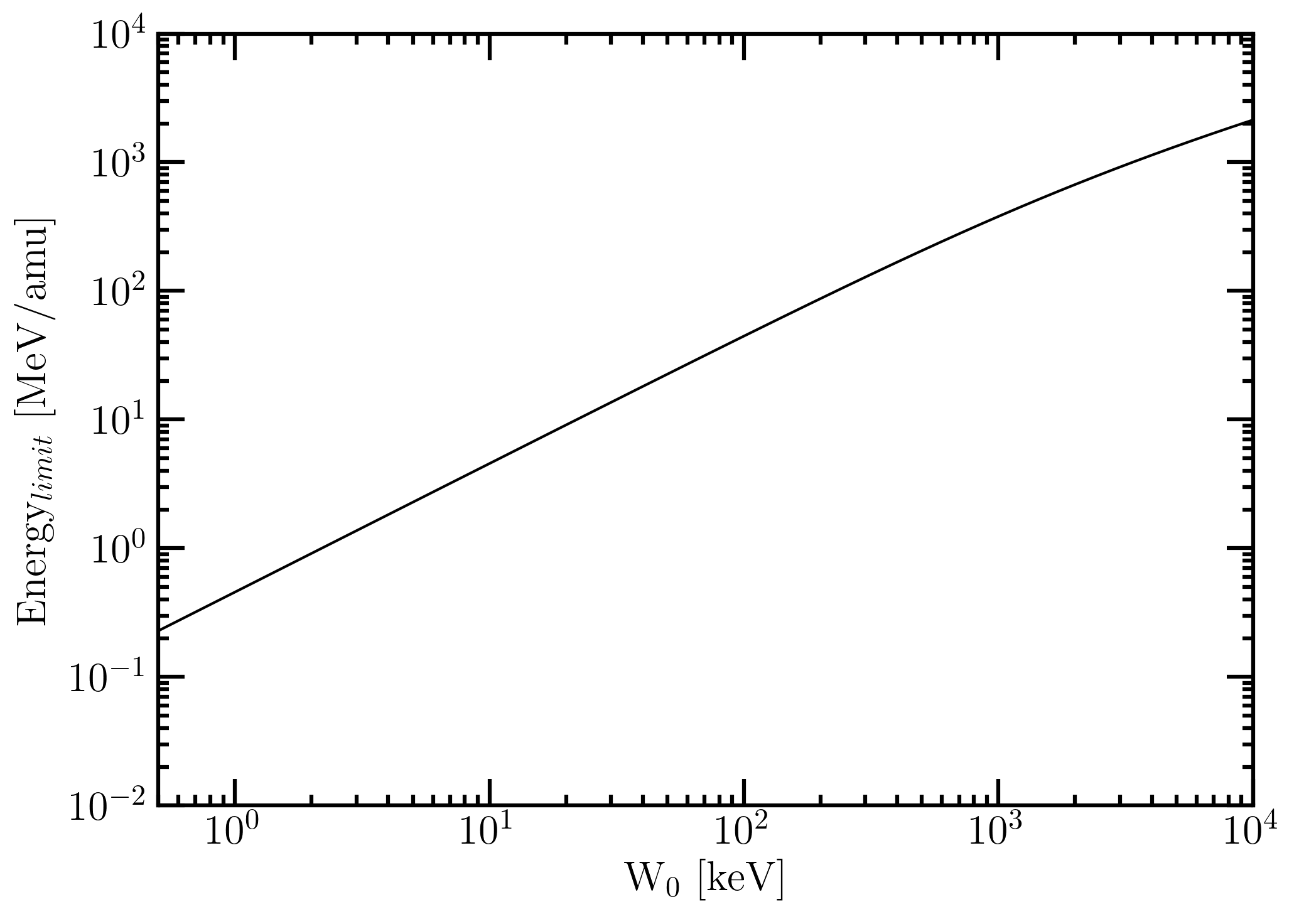
Figure 1. Energy limit (in MeV/amu) below which there is no difference in between the SR-Framework electronic stopping power and the restricted energy loss as a function of W0.
Incident Particle
In the calculator panel, using the pull down menu, the user can select the species of the incident particle, either a proton or one of the elemental ions.
The user can also modify the mass (in amu) of the incident particle (e.g., for all isotopes one can refer to this page): the default mass is that of the most abundant isotope (MAI), except for proton and alpha particle masses. Further information are available at the following webpage.
Spectral Fluence
These data (from the user) provide the spectral fluence as a function of energy.
This section define the points of the spectral fluence as a function of energy.
The input format is one point per line (Energy - Flux , separated by a space or tab); it is also possible to copy and paste values. The minimum value of the particle spectral fluence is 1 eV.
In addition, incoming particle directions have to be identical to those employed in measuring the SEE cross section, so that the traversed path inside the device is not modified.
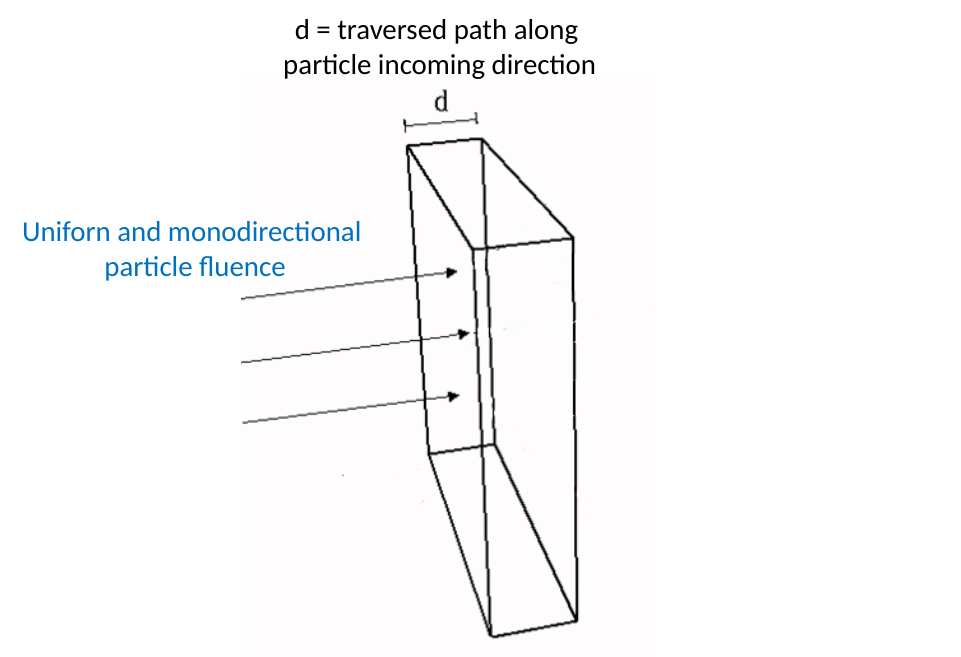
One has to remark (see webpage) how the physical mechanism of energy deposition per unit length in a medium is such that the resulting computed value of restricted energy loss depends on the overall traversed path to which W0 is related. The electronic stopping power, on the other hand, does not depend on the incoming particle direction with respect to the medium surface.
Result
The result page contains the input spectral fluence and the SEE cross section as a function of energy. The spectral fluence is interpolated and divided in 1000 energy bins to obtain the total number of SEE. The calculation is performed with three types of stopping power (SRIM, SR electronic stopping power and Restricted energy loss). The energy, fluence, cross section and spectral number of SEE are reported in the table.