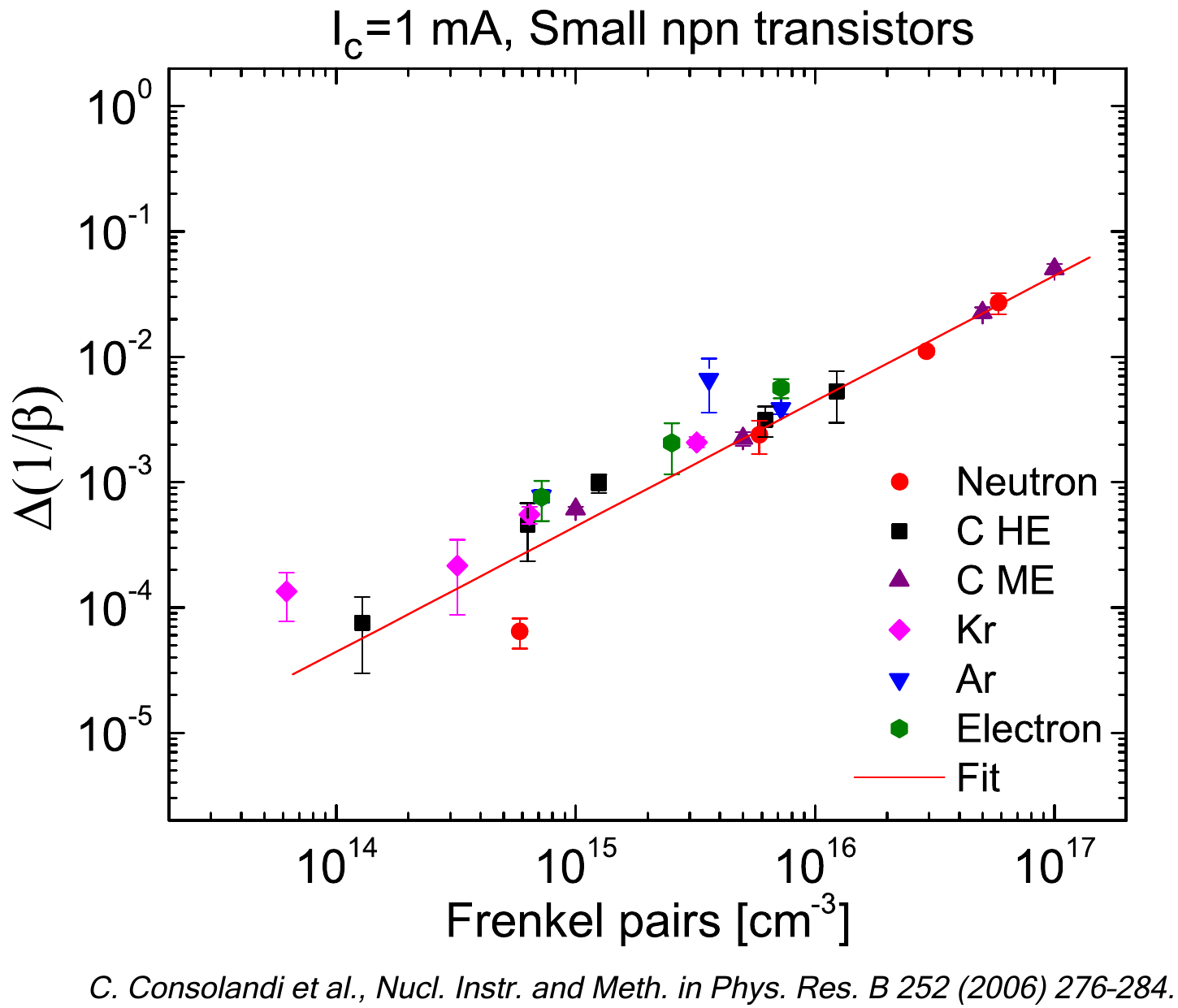
A relevant process - which causes permanent damage to the silicon bulk structure - is the so-called displacement damage (e.g., see Chapter 7 of [Leroy and Rancoita (2016)], see also [Consolandi et al. (2006), Leroy and Rancoita (2007), Boschini et al. (2011), Boschini et al. (2012)] and references therein). Displacement damage may be inflicted when a primary knocked-on atom (PKA) is generated. The interstitial atom and relative vacancy are termed Frenkel-pair (FP). In turn, the displaced atom may have sufficient energy to migrate inside the lattice and - by further collisions - can displace other atoms as in a collision cascade. This displacement process modifies the bulk characteristics of the device and causes its degradation. The total number of FPs can be estimated calculating the energy density deposited from displacement processes. In turn, this energy density is related to the non-ionizing energy loss (NIEL), i.e., the energy per unit path lost by the incident particle due to displacement processes.
For instance, in Chapter 2 and of [Leroy and Rancoita (2016)] (see also [Boschini et al. (2012)] and references therein), the differential cross section for electron–nucleus scattering was dealt to describe their interaction up to ultra high-energy and, in addition, it was accounting (above about 200 keV) for the effects due to the screening of Coulomb potentials, finite sizes and finite rest masses of target nuclei. In fact, it has to be remarked - as derived by Zeitler and Olsen ([Zeitler and Olsen (1956)]) - that spin and screening effects can be separately treated for small scattering angles; while at large angles (i.e., at large momentum transfer), the factorization is well suited under the condition that

(e.g., see [Zeitler and Olsen (1956), Idoeta and Legarda (1992)]). Zeitler and Olsen suggested that for electron energies above 200 keV the overlap of spin and screening effects is small for all elements and for all energies; for lower energies the overlapping of the spin and screening effects may be appreciable for heavy elements and large angles. Furthermore, to a first approximation, the finite nuclear size effects can be accounted for by means of the nuclear form factor (e.g., see Eqs. (2.262, 2.264, 2.265) of [Leroy and Rancoita (2016)] and discussion in Sect. 2.4.2.1), for instance, the so called exponential form factor (Fexp) expressed by Eq. (2.262) of [Leroy and Rancoita (2016)].
The previously mentioned treatment allows one to obtain the nuclear stopping power for electrons in materials. Furthermore, within such a framework, Boschini and collaborators (2012) calculated the non-ionizing energy-loss using the Mott differential cross section (MDCS), dσsc,F,CoMMott(T)∕dT dT, and its approximate expression, i.e., the McKinley and Feshbach differential cross section (McFDCS), dσsc,F,CoMMcF (T)∕dT, so that also the screened Coulomb fields, finite sizes and rest masses of nuclei were taken into account. It has to be remarked that, in the current treatment for the MDCS, Boschini and collaborators (2013) derived an improved numerical approach and an interpolated expression (e.g., see Sections 2.4.1–2.4.2 of [Leroy and Rancoita (2016)] and [Boschini et al. (2013)]) for the cross-section. For instance, one finds that the NIEL in units of MeV/cm is derived as:
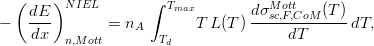 | (1) |
or
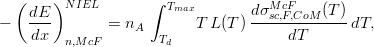 | (2) |
where T is the kinetic energy transferred to the target nucleus, L(T) is the fraction of T deposited by means of displacement processes. The Lindhard partition function, L(T), can be approximated using the so-called Norgett–Robintson–Torrens expression [e.g., [Jun (2001), Messenger et al. (2003)] and/or Equations (7.20, 7.28) at pages 489 and 490, respectively, of [Leroy and Rancoita (2007)] (see also references therein)]. Tde = T L(T) is the so-called damage energy, i.e., the energy deposited by a recoil nucleus with kinetic energy T via displacement damages inside the medium. In Eqs. (1, 2) the integral is computed from the minimum energy Td - the so-called threshold energy for displacement, i.e., that energy necessary to displace the atom from its lattice position - up to the maximum energy Tmax that can be transferred during a single collision process. For instance, Td is about 21 eV in silicon (e.g., see Table 1 in [Jun, Xapsos, Messenger, Burke, Walters, Summers and Jordan (2003)] and references therein) requiring electrons with kinetic energies above ≈ 220 keV [e.g., see Equation (7.51) at page 501 of [Leroy and Rancoita (2007)]].
As known, the large momentum transfers (corresponding to large scattering
angles) are disfavored by effects due to the finite nuclear size accounted for
by the nuclear form factor. For instance, in Fig. 1 the ratios of NIELs
for electrons in silicon are shown as a function of the kinetic energy of
electrons from 220 keV up to 1 TeV. These ratios are the NIELs calculated
neglecting i) nuclear size effects (i.e., for 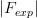 2 = 1) and ii) effects due
to the finite rest mass of the target nucleus both divided by that one
(Fig. 2) obtained using Eq. (2). Above ≈ 10 MeV, the NIEL is ≈ 20%
larger assuming
2 = 1) and ii) effects due
to the finite rest mass of the target nucleus both divided by that one
(Fig. 2) obtained using Eq. (2). Above ≈ 10 MeV, the NIEL is ≈ 20%
larger assuming 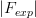 2 = 1 and, in addition, above (100–200) MeV the
calculated NIEL largely decreases when the effects of nuclear rest mass
are not accounted for (for a detailed discussion, for instance, one may
see Section 7.1.1.8 in [Leroy and Rancoita (2007)]). Finally, it has to be
remarked that similar results can be obtained neglecting the screening factor:
already at energies lower that 200 keV, Td ≈ 21 eV is much larger than
TmaxAs.
2 = 1 and, in addition, above (100–200) MeV the
calculated NIEL largely decreases when the effects of nuclear rest mass
are not accounted for (for a detailed discussion, for instance, one may
see Section 7.1.1.8 in [Leroy and Rancoita (2007)]). Finally, it has to be
remarked that similar results can be obtained neglecting the screening factor:
already at energies lower that 200 keV, Td ≈ 21 eV is much larger than
TmaxAs.
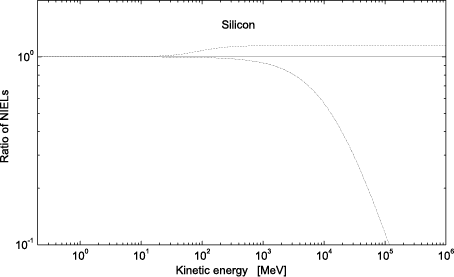
From Boschini and collaborators (2012), for Td = 21 eV, ratios of
NIELs of electrons in silicon calculated as a function of the kinetic energy of
electrons from 220 keV up to 1 TeV neglecting i) nuclear size effects (i.e., for
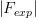 2 = 1) (dashed curve) and ii) effects due to the finite rest mass of the
target nucleus (dashed and dotted curve) [e.g. see [Boschini et al. (2012)]]
both divided by that one obtained using Eq. (2).
2 = 1) (dashed curve) and ii) effects due to the finite rest mass of the
target nucleus (dashed and dotted curve) [e.g. see [Boschini et al. (2012)]]
both divided by that one obtained using Eq. (2).
In Fig. 2, for Td = 21 eV the non-ionizing energy loss (in MeV cm2 g-1) calculated using Eq. (2) in silicon is shown (dashed and dotted curve) as a function of the kinetic energy from 220 keV up to 1 TeV and is compared with that one tabulated by Messenger et al.[Messenger et al. (1999)] (Jun et al.[Jun, Kim and Evans (2009)]) from ≈ 240 keV up to 200 MeV (1 GeV). For the laboratory system, Messenger et al.[Messenger et al. (1999)] used the approximate MDCS found by Doggett-Spencer[Doggett and Spencer (1956))] and Lindhard’s partition function numerically obtained by Doran[Doran (1972] without accounting for the effects due to screened Coulomb potential (i.e., 𝔉2 = 1), finite size (i.e., F2 = 1) and finite rest mass of the silicon target; while, Jun et al.[Jun, Kim and Evans (2009)] followed the approach discussed in [Lijian, Quing and Zhengming (1995)] to determine an approximate expression of the MDCS and dealt the Lindhard partition function using the modified Norgett–Robintson–Torrens expression found2 by Akkerman and Barak (2006). The dotted curve is obtained replacing dσsc,F,CoMMcF (T)∕dT with dσMcF (T)∕dT [ i.e., that one not accounting for accounting for the effects due to the screened Coulomb potential, finite size and rest mass of recoil silicon] in Eq. (2): at 100 MeV–1 GeV, the agreement between the latter calculation and values from Messenger et al.[Messenger et al. (1999)] and Jun et al.[Jun, Kim and Evans (2009)] is within several percents. It has to be remarked (see also Fig. 1) that i) above (100–200) MeV effects due to screened Coulomb potentials, finite sizes and finite rest masses of nuclei have to be taken into account and ii) for energies between ≈ 100 MeV and ≈ 1 GeV the effects of neglecting the nuclear form factor and finite rest mass of nuclei almost compensate each other.

From Boschini and collaborators (2012), for Td = 21 eV, NIEL (in MeV cm2 g-1) in silicon calculated using Eq. (2) as a function of the kinetic energy from 220 keV up to 1 TeV (dashed and dotted curve); NIEL values from Messenger et al.[Messenger et al. (1999)] (∘) and Jun et al.[Jun, Kim and Evans (2009)] (∙) calculated in the laboratory system without accounting for effects due to screened Coulomb potential, finite size and rest mass of recoil silicon; the dotted curve is obtained replacing dσsc,F,CoMMcF (T)∕dT with dσMcF (T)∕dT, i.e., that one not accounting for the effects due to the screened Coulomb potential, finite size and rest mass of recoil silicon.
References
[Akkerman and J. Barak (2006)] A. Akkerman and J. Barak (2006), IEEE Trans. on Nucl. Sci. vol. 53, 3667–3674.
[Boschini et al. (2011)] M.J. Boschini, C. Consolandi, M. Gervasi, S. Giani, D. Grandi, V. Ivantchenko, S. Pensotti, P.G. Rancoita, M. Tacconi, Nuclear and Non-Ionizing Energy-Loss for Coulomb Scattered Particle from Low Energy up to relativistic regime in Space Radiation Environment, Proc. of the 12th ICATPP Conference, October 7-8 2010, Villa Olmo, Como, Italy, World Scientific, Singapore (2011), 9-23, IBSN: 978-981-4329-02-6; http://www.worldscientific.com/doi/pdf/10.1142/9789814329033_0002 or http://arxiv.org/pdf/1011.4822v7.pdf.
[Boschini et al. (2012)] M.J. Boschini, C. Consolandi, M. Gervasi, S. Giani, D. Grandi, V. Ivanchenko, P. Nieminem, S. Pensotti, P.G. Rancoita and M. Tacconi, Nuclear and Non-Ionizing Energy-Loss of electrons with low and relativistic energies in materials and space environment, Proc. of the 13th ICATPP Conference, October 3-7 2011, Villa Olmo, Como, Italy, World Scientific, Singapore (2012), 961-982, IBSN: 978-981-4405-06-5; http://www.worldscientific.com/doi/pdf/10.1142/9789814405072˙0147; http://arxiv.org/pdf/1111.4042v4.pdf
[Boschini et al. (2013)] M.J. Boschini, C. Consolandi, M. Gervasi, S. Giani, D. Grandi, V. Ivanchenko, P. Nieminem, S. Pensotti, P.G. Rancoita, M. Tacconi (2013), An expression for the Mott cross section of electrons and positrons on nuclei with Z up to 118, Rad. Phys. Chem. 90, 39-66; doi: 10.1016/j.radphyschem.2013.04.020, http://www.sciencedirect.com/science/article/pii/S0969806X13002454; http://arxiv.org/pdf/1304.5871v1.pdf
[Consolandi et al. (2006)] C. Consolandi, P.D’Angelo, G. Fallica, R. Modica, R. Mangoni, S. Pensotti and P.G. Rancoita (2006), Systematic Investigation of Monolithic Bipolar Transistors Irradiated with Neutrons, Heavy Ions and Electrons for Space Applications, Nucl. Instr. and Meth. in Phys. Res. B 252 (2006), 276, doi:10.1016/j.nimb.2006.08.018; http://www.sciencedirect.com/science/article/pii/S0168583X0600913X.
[Doggett and Spencer (1956))] J.A. Doggett and L.V. Spencer (1956), Phys. Rev. 103, 1597-1601.
[Doran (1972] D.G. Doran (1972), Nucl. Sci. Eng. 49, 130–144.
[Idoeta and Legarda (1992)] R. Idoeta and F. Legarda (1992, Nucl. Instr. and Meth. in Phys. Res. B 71), 116–125.
[Jun (2001)] I. Jun (2001), IEEE Trans. on Nucl. Sci. 48, 162–175.
[Jun, Kim and Evans (2009)] I. Jun, W. Kim and R. Evans (2009), IEEE Trans. on Nucl. Sci. vol. 56, 3229–3235.
[Jun, Xapsos, Messenger, Burke, Walters, Summers and Jordan (2003)] I. Jun, M.A Xapsos, S.R. Messenger, E.A. Burke, R.J. Walters, G.P. Summers and T. Jordan (2003), IEEE Trans. on Nucl. Sci. 50, 1924–1928.
[Leroy and Rancoita (2007)] C. Leroy and P.G. Rancoita (2007), Particle Interaction and Displacement Damage in Silicon Devices operated in Radiation Environments Reports on Progress in Physics 70, 493-625, doi:10.1088/0034-4885/70/4/R0; http://iopscience.iop.org/0034-4885/70/4/R01/.
[Leroy and Rancoita (2016)] C. Leroy and P.G. Rancoita (2016), Principles of Radiation Interaction in Matter and Detection - 4th Edition -, World Scientific. Singapore, ISBN-978-981-4603-18-8 (printed); ISBN.978-981-4603-19-5 (ebook); https://www.worldscientific.com/worldscibooks/10.1142/9167#t=aboutBook; it is also partially accessible via google books.
[Lijian, Quing and Zhengming (1995)] T. Lijian, H. Quing and L. Zhengming (1995), Radiat. Phys. Chem. 45, 235–245.
[Messenger et al. (1999)] S.R. Messenger et al. (1999), IEEE Trans. on Nucl. Sci. vol. 46, no. 6, 1595-1601.
[Messenger et al. (2003)] S.R. Messenger et al. (2003), IEEE Trans. on Nucl. Sci. 50, 1919–1923.
[Zeitler and Olsen (1956)] E. Zeitler and A. Olsen (1956), Phys. Rev. 136, A1546-A1552.
2Jun et al. (2009) determined that the usage of the Norgett–Robintson–Torrens expression or, alternatively, the one modified by Akkerman and Barak (2006) yields similar NIEL values.