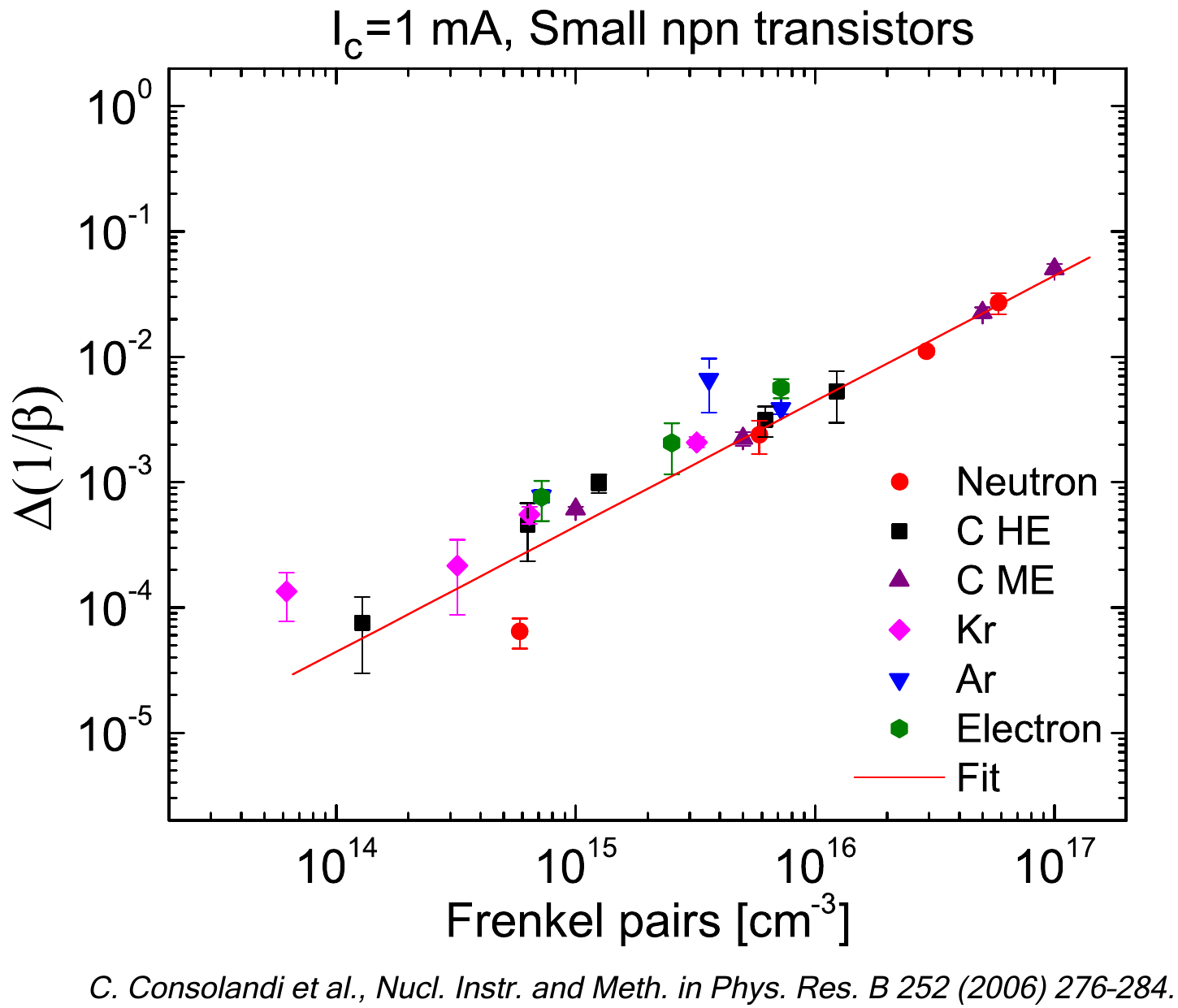
A relevant process - which causes permanent damage to the silicon bulk structure - is the so-called displacement damage (e.g., see Chapter 7 of [Leroy and Rancoita (2016)], see also [Borchi et al. (1989), Consolandi et al. (2006), Leroy and Rancoita (2007)] and references therein). Displacement damage may be inflicted when a primary knocked-on atom (PKA) is generated. The interstitial atom and relative vacancy are termed Frenkel-pair (FP). In turn, the displaced atom may have sufficient energy to migrate inside the lattice and - by further collisions - can displace other atoms as in a collision cascade. This displacement process modifies the bulk characteristics of the device and causes its degradation. The total number of FPs can be estimated calculating the energy density deposited from displacement processes. In turn, this energy density is related to the Non-Ionizing Energy Loss (NIEL), i.e., the energy per unit path lost by the incident particle due to displacement processes.
Above 50 keV/nucleon (e.g., see here), in case of Coulomb scattering on nuclei (the reader can refer to Sections 2.2–2.2.2, 7.1–7.1.1.6 of [Leroy and Rancoita (2016)] for a comprehensive treatment) the non-ionizing energy-loss can be calculated using the Wentzel–Molière differential cross section:
![dσW M (T ) ( 2)2 E2 1
----------= 2π zZe -2----4--------------2,
dT p M c [Tmax As + T ]](/images/images_handbook/niellprotonandion0x.png) | (1) |
discussed, for instance, in [Boschini et al. (2011)] and Section 2.2.2 of [Leroy and Rancoita (2016)], i.e.,
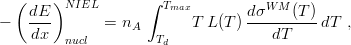 | (2) |
where E is the kinetic energy of the incoming particle, T is the kinetic energy transferred to the target atom, L(T) - the so-called Lindhard partition function - is the fraction of T deposited by means of displacement processes. An analytical approximation of L(T) - the so-called Norgett-Robinson-Torrens expression - can be found, for instance, in [Jun (2001), Messenger et al. (2003)]] and in Equations (7.26, 7.27) of Sections 7.1.1.1 and 7.1.1.2 in [Leroy and Rancoita (2016)] (see also references therein). Tde = T L(T) is the so-called damage energy, i.e., the energy deposited by a recoil nucleus with kinetic energy T via displacement damages inside the medium. The integral in Eq. (2) is computed from the minimum energy Td - the so-called threshold energy for displacement, i.e., that energy necessary to displace permanently the atom from its lattice position - up to the maximum energy Tmax that can be transferred during a single collision process. Td is about 21 eV in silicon (e.g., see Table 1 in [Jun, Xapsos, Messenger, Burke, Walters, Summers and Jordan (2003)] and references therein) and 25 eV in lead (e.g., see Table 22 at page 83 in [Was (2007)] and references therein). As already remarked by Boschini and collaborators (2011), at high energy the Coulomb NIEL - similarly to the nuclear stopping power - does not decrease with energy as it is found by Ziegler, Biersack and Littmark (1985) or in other calculations based on their universal screening potential derived in the framework of a non-relativistic treatment of the screened Coulomb scattering.
For energies lower than 50-200 keV/nucleon, the scattering of protons and screened nuclei can be treated using the 4-terms analytical approximation of the ZBL cross section derived by Messenger et al. (2004) [see Eqs. (1--3, 15) and also references therein].
Furthermore, Jun and collaborators (2003) demonstrated that a relativistic treatment [Jun (2001)] of Coulomb scattering of protons - with kinetic energies above 50 MeV - upon silicon results into a non-ionizing energy loss which is larger than that expected from calculations using the Ziegler–Biersack–Littmark screened potential with a universal screening length (e.g., see [Ziegler, Biersack and Littmark (1985), Jun, Xapsos, Messenger, Burke, Walters, Summers and Jordan (2003), Messenger et al. (2003)]). The relativistic cross section used for treating the Coulomb scattering is the one derived by McKinley and Feshbach (1948) to describe the scattering of electrons on nuclei (e.g., see Sections 2.4.1, 7.1.1.7 of [Leroy and Rancoita (2016)] and references therein). Seitz and Koehler (1956) suggested that - when the mass of the projectile is much lower than the target rest-mass (e.g., see Section 13 of [Seitz and Koehler (1956)] and references therein) - this cross section can also describe - although screening effects are neglected - the scattering of protons and light nuclei, thus, providing - at high energy - a damage cross section which does not decrease with increasing energy. The data from Jun and collaborators (2003) - for protons with energies from 100 keV up to 1 GeV - are shown in Fig.1: the Ziegler–Biersack–Littmark (1985) screened potential was used to treat the Coulomb scattering of protons with energies lower than 50 MeV. In the same figure, the data obtained using Eq. (2) are also shown. There is an agreement to better than ≈ 6.5% - achieved at ≈ 1 GeV - between the results obtained by Jun and collaborators (2003) and the present screened relativistic (sr) calculations.
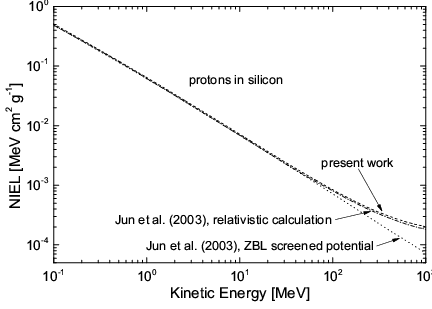
Non-ionizing stopping powers of protons in silicon with energies from 100 keV up to 1 GeV (from [Boschini et al. (2011)]): data for the dashed-dotted and dotted lines are the relativistic and Ziegler-Biersack-Littmark screened potential calculations from Jun and collaborators (2003), respectively (e.g., see [Jun, Xapsos, Messenger, Burke, Walters, Summers and Jordan (2003)]); data for the dashed line are obtained from Eq. (2).
References
[Borchi et al. (1989)] E. Borchi et al., Nucl. Instr. and Meth. in Phys. Res. A 279 (1989), 277–280.
[Boschini et al. (2011)] M.J. Boschini, C. Consolandi, M. Gervasi, S. Giani, D. Grandi, V. Ivantchenko, S. Pensotti, P.G. Rancoita, M. Tacconi, Nuclear and Non-Ionizing Energy-Loss for Coulomb Scattered Particle from Low Energy up to relativistic regime in Space Radiation Environment, Proc. of the 12th ICATPP Conference, October 7-8 2010, Villa Olmo, Como, Italy, World Scientific, Singapore (2011), 9-23, IBSN: 978-981-4329-02-6; http://www.worldscientific.com/doi/pdf/10.1142/9789814329033_0002 or http://arxiv.org/pdf/1011.4822v7.pdf.
[Consolandi et al. (2006)] C. Consolandi, P.D’Angelo, G. Fallica, R. Modica, R. Mangoni, S. Pensotti and P.G. Rancoita, Systematic Investigation of Monolithic Bipolar Transistors Irradiated with Neutrons, Heavy Ions and Electrons for Space Applications, Nucl. Instr. and Meth. in Phys. Res. B 252 (2006), 276, doi:10.1016/j.nimb.2006.08.018; http://www.sciencedirect.com/science/article/pii/S0168583X0600913X.
[Jun (2001)] I. Jun, IEEE Trans. on Nucl. Sci. 48 (2001), 162–175
[Jun, Xapsos, Messenger, Burke, Walters, Summers and Jordan (2003)] I. Jun, M.A Xapsos, S.R. Messenger, E.A. Burke, R.J. Walters, G.P. Summers and T. Jordan, IEEE Trans. on Nucl. Sci. 50 (2003), 1924–1928.
[Leroy and Rancoita (2007)] C. Leroy and P.G. Rancoita (2007), Particle Interaction and Displacement Damage in Silicon Devices operated in Radiation Environments Reports on Progress in Physics 70, 493-625, doi:10.1088/0034-4885/70/4/R0; http://iopscience.iop.org/0034-4885/70/4/R01/.
[Leroy and Rancoita (2016)] C. Leroy and P.G. Rancoita (2016), Principles of Radiation Interaction in Matter and Detection - 4th Edition -, World Scientific. Singapore, ISBN-978-981-4603-18-8 (printed); ISBN.978-981-4603-19-5 (ebook); https://www.worldscientific.com/worldscibooks/10.1142/9167#t=aboutBook; it is also partially accessible via google books.
[Messenger et al. (2003)] S.R. Messenger et al., IEEE Trans. on Nucl. Sci. 50 (2003), 1919–1923.
[Messenger et al. (2004)] S.R. Messenger et al., IEEE Trans. on Nucl. Sci. 51 (2004), 2846–2850.
[McKinley and Feshbach (1948)] A.Jr. McKinley and H. Feshbach Phys. Rev. 74 (1948), 1759.
[Seitz and Koehler (1956)] F. Seitz and J.S. Koehler, Solid State Physics vol. 2, edited by F. Seitz and D. Turnbull, Academic Press Inc. (New York), 1956.
[Was (2007)] G.S. Was, Fundamentals of radiation materials science: metals and alloys Springer (Berlin), 2007.
[Ziegler, Biersack and Littmark (1985)] J.F. Ziegler, J.P. Biersack and U. Littmark, The Stopping Range of Ions in Solids, Vol. 1, Pergamon Press (New York) 1985.