The following text is based on / extracted from Section 2.1.1.4 of [Leroy and Rancoita (2016)]:
In the following Fig. 1 experimental data for incoming massive particles with z=1 - collected with silicon detectors - exhibit the approach of the deposited energy to the Fermi plateau (see also Figure 33.6 at page 450 in Tanabashi et al. - Particle Data Group - (2018)). The escaped δ-rays result in a lower measured energy-loss deposition (i.e., deposited energy) with respect to that expected from the energy-loss formula [see Eq. (2.18) at page 61 of [Leroy and Rancoita (2016)]]. For instance, at the energy-loss minimum [see Eq. (2.22) at page 66 of [Leroy and Rancoita (2016)]] and for z=1, the calculated value of −(dE/dx) in silicon is ≈ 3.87 MeV/cm (equivalently ≈ 387 eV/μm) and is in agreement with the one given in Section 6 of [PDB (2014)] (see also references therein). For the 900 μm thick silicon detector of [Esbensen et al. (1978); Rancoita (1984)], the value of W0 is ≈ 0.5 MeV and the restricted energy-loss value - calculated from Eq. (2.32) at page 71 of of [Leroy and Rancoita (2016)] - is ≈ 345 eV/μm, in agreement with the experimental data shown in Fig. 1.
Since a device is usually not thick enough to fully absorb secondary δ-rays, the energy loss suffered by the incoming particle differs from the one deposited inside the detecting medium. As a consequence, the escaped δ-rays result in an effective detectable maximum transferred energy and, in turn, the deposited energy will reach a constant value, called the Fermi plateau.
It has to be remarked that, by an inspection of Fig. 1, the Fermi plateau calculated by means of Eq. (2.33) at page 71 of of [Leroy and Rancoita (2016)] is only ≈ 10 eV/μm higher than the restricted energy-loss at the minimum: in dense media like silicon, the relativistic rise may become almost negligible. In silicon detectors, the active layer thickness is typically (300–400) μm and, thus, it can absorb δ-rays with kinetic energies not exceeding ≈ 300 keV (e.g., see page 132 of of [Leroy and Rancoita (2016)] ). However, as mentioned above, 900 μm thick absorbers were also used. For instance, the maximum transferred kinetic energy is ≈ 0.3 (0.5) MeV for a proton with kinetic energy of ≈ 128 (207) MeV, i.e., with βγ ≈ 0.54 (0.70). Therefore, the non-complete absorption of emitted δ-rays is expected to affect the energy-deposition curve in silicon detectors for incoming protons (or other heavy charged particles) with βγ larger than about 0.54–0.70.
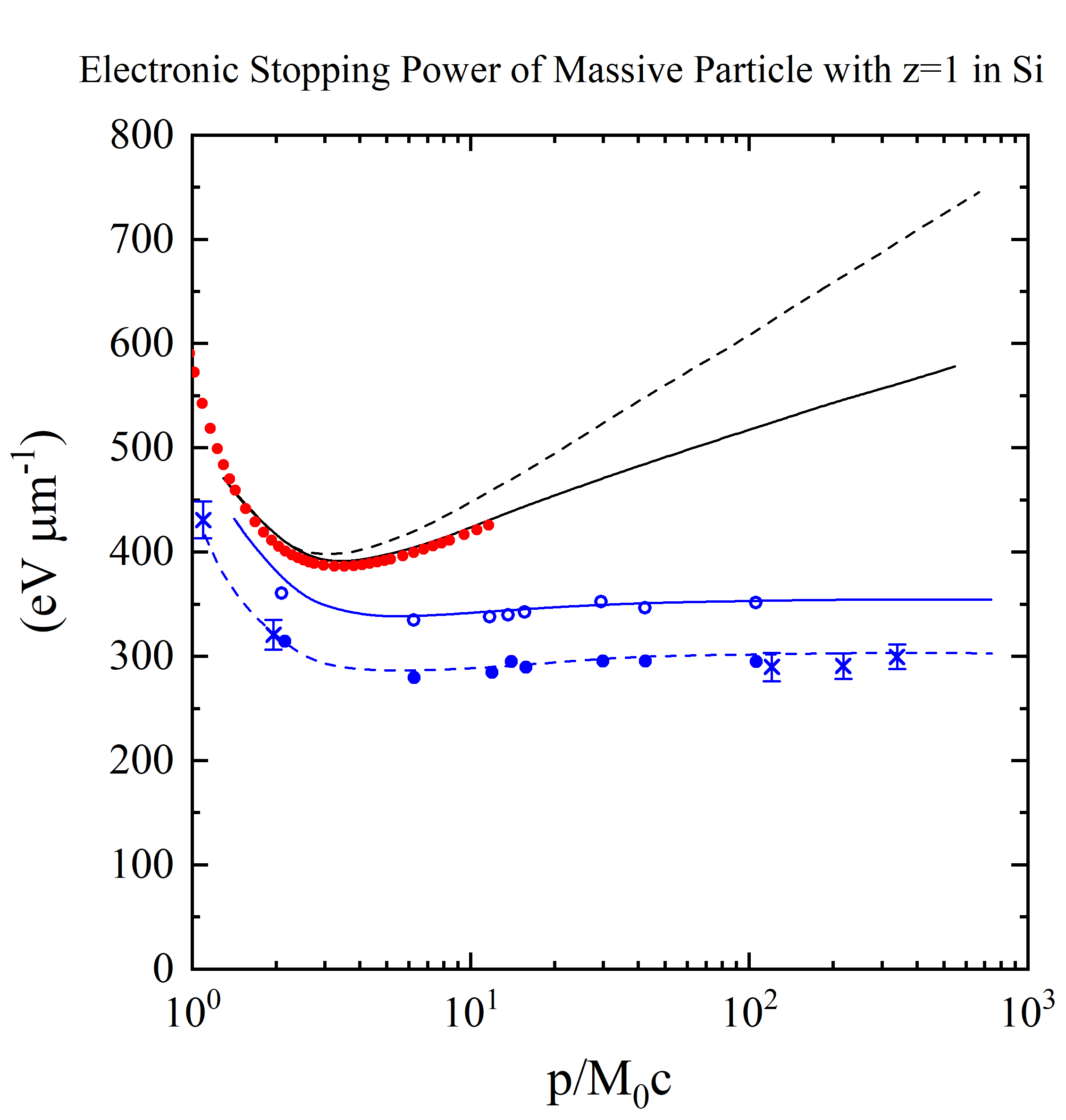 Figure 1. Energy loss in silicon (in units of eV/μm) versus βγ (= p/M0c, where M0 and p are the rest mass and the momentum of the incoming particle with z=1) from [Rancoita (1984)]. From the top, the first two curves are: the stopping power without (broken curve) and with (full curve) the density-effect correction (e.g. see chapter 2 of [Leroy and Rancoita (2016)]) . The red points for incoming protons up to 10 GeV (βγ =11.61) are obtained from present electronic stopping power SRIM calculator implemented in this website. The following two other curves - compared to experimental data for detector thicknesses of 300 (× from [Hancock, James, Movchet, Rancoita and Van Rossum (1983)]) and 900 μm (◦ and • from [Esbensen et al. (1978)]) - are, respectively, i ) the top one (solid line in blue) for the restricted energy-loss with the density-effect taken into account and ii) the bottom one (dashed line in blue) for prediction of the most probable energy-loss. Furthermore (as discussed at page 82 of [Leroy and Rancoita (2016)]), for βγ > 100, in 300 μm thick silicon detector the observed most probable energy-loss (in eV/μm) is about 5% lower than that in 900 μm thick silicon detetor in agreement, within the experimental errors, with the decrease of about 6.5% calculated by means of Eq. (2.56) at page 81 of [Leroy and Rancoita (2016)].
Figure 1. Energy loss in silicon (in units of eV/μm) versus βγ (= p/M0c, where M0 and p are the rest mass and the momentum of the incoming particle with z=1) from [Rancoita (1984)]. From the top, the first two curves are: the stopping power without (broken curve) and with (full curve) the density-effect correction (e.g. see chapter 2 of [Leroy and Rancoita (2016)]) . The red points for incoming protons up to 10 GeV (βγ =11.61) are obtained from present electronic stopping power SRIM calculator implemented in this website. The following two other curves - compared to experimental data for detector thicknesses of 300 (× from [Hancock, James, Movchet, Rancoita and Van Rossum (1983)]) and 900 μm (◦ and • from [Esbensen et al. (1978)]) - are, respectively, i ) the top one (solid line in blue) for the restricted energy-loss with the density-effect taken into account and ii) the bottom one (dashed line in blue) for prediction of the most probable energy-loss. Furthermore (as discussed at page 82 of [Leroy and Rancoita (2016)]), for βγ > 100, in 300 μm thick silicon detector the observed most probable energy-loss (in eV/μm) is about 5% lower than that in 900 μm thick silicon detetor in agreement, within the experimental errors, with the decrease of about 6.5% calculated by means of Eq. (2.56) at page 81 of [Leroy and Rancoita (2016)].
References
[Leroy and Rancoita (2016)] C. Leroy and P.G. Rancoita (2016), Principles of Radiation Interaction in Matter and Detection - 4th Edition -, World Scientific. Singapore, https://www.worldscientific.com/worldscibooks/10.1142/9167#t=aboutBook; ISBN-978-981-4603-18-8 (printed); ISBN.978-981-4603-19-5 (ebook); it is also partially accessible via google books.
[PDB (2014)] PDB (2014): Olive, K.,A. et al. (Particle Data Group) (2014). Review of Particle Physics,Chin. Phys. C 38, 090001. The latest versions of tables, reference data and constants are available at the Particle Data Group website:http://http://pdg.lbl.gov/
[Esbensen et al. (1978)] Esbensen, H. et al. (1978). Phys. Rev. B 18, 1039.
[Rancoita (1984)] Rancoita, P.G. (1984). Silicon detectors and elementary particle physics, J. Phys. G: Nucl.Phys. 10, 299–319, doi: 10.1088/0305-4616/10/3/007.
[Hancock, James, Movchet, Rancoita and Van Rossum (1983)] Hancock, S., James, F., Movchet, J., Rancoita, P.G. and Van Rossum, L. (1984). Nucl. Instr. and Meth. in Phys. Res. B 1, 16, doi: 10.1016/0168-583X(84)90472-5.
[M. Tanabashi et al. (Particle Data Group)] Phys. Rev. D 98, 030001 – Published 17 August 2018 https://journals.aps.org/prd/abstract/10.1103/PhysRevD.98.030001