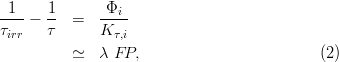As discussed in Sections 7.4–7.4.1 of [Leroy and Rancoita (2016)] (see also [Leroy and Rancoita (2007)]), among the most important semiconductor material-parameters for practical applications in electronic devices, we have the (excess-) carrier lifetime (e.g. see [Schroder (1997)]), the equilibrium majority-carrier concentration and the majority-carrier mobility. To a first approximation1, the rate at which the electrical properties of semiconductors degrade by irradiation is often expressed in terms of a damage coefficient. For instance, the minority carrier (recombination) lifetime (τ) is given by
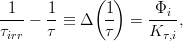 | (1) |
where τirr and τ are the lifetimes after and before the irradiation with a fluence Φi of particles, respectively; Kτ,i is the (recombination) lifetime damage coefficient2, which may depend on i) the type of substrate, ii) the dopant concentration, iii) the level of compensation and iv) the type (“i”) and energy of irradiating particles (e.g., see Section 5 in Chapter I of Part II of [Vavilov and Ukhin (1977)], [Srour and McGarrity (1988)], Section 3.4 of [Srour, Long, Millward, Fitzwilson and Chadsey (1984)] and references therein). Values of Kτ,i are available in literature. For instance, for low-resistivity silicon experimental results on the lifetime damage constants are presented in [Srour, Othmer and Chiu (1975)] for 0.5, 1.0 and 2.5 MeV electrons with fluences up to ≃ 3 × 1015 e/cm2 and 10 MeV protons with fluences up to ≃ 1.2 × 1012 p/cm2 (see also Section 3.4 of [Srour, Long, Millward, Fitzwilson and Chadsey (1984)]).
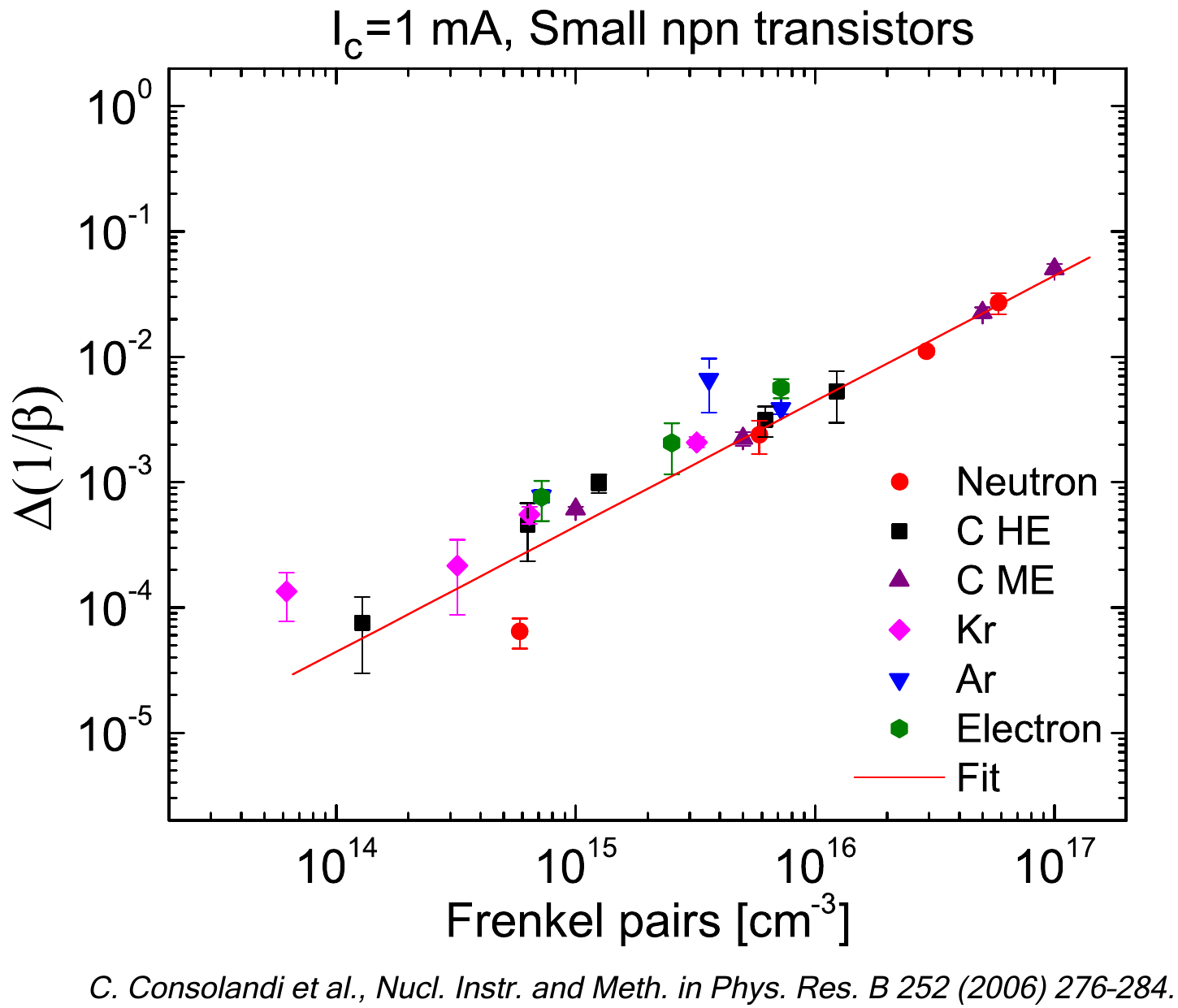
To a first approximation (e.g., see discussion in Sections 7.4.1, 11.1.2, 11.1.4., 11.4.1.1 of [Leroy and Rancoita (2016)]), in absence of saturation effects3, (mostly) for low-resistivity silicon we can assume that the concentration of recombination centers is proportional – although the proportionality constant may be slightly varied, in particular, when the cascades of primary defects induced by recoil nuclei are largely different – to the energy deposited by non-ionizing energy-loss (NIEL) processes per unit volume Edis and, consequently, to the concentration of Frenkel-pairs (FP) introduced as primary point-defects. Furthermore, as treated in Section 7.4.1 of [Leroy and Rancoita (2016)], one can derive that Eq. (1) can be re-written as:
where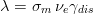
is almost – under the above mentioned assumptions – independent of the type
and energy of the incoming particle, but depends on i) the type of substrate, ii)
(slightly) the dopant concentration and iii) the level of compensation and, where,
ve is the average speed of minority carriers, σm is the cross section for the
absorption of minority carriers by recombination centers and γdis expresses the
proportionality constant between the deep defect concentration and that of
Frenkel-pairs FP. Equations (2) indicates that an approximate NIEL scaling is
expected for the variation of the reciprocal of the minority-carrier lifetime in
low-resistivity silicon.
References
[Leroy and Rancoita (2007)] C. Leroy and P.G. Rancoita (2007), Particle Interaction and Displacement Damage in Silicon Devices operated in Radiation Environments Reports on Progress in Physics 70, 493-625, doi:10.1088/0034-4885/70/4/R0; http://iopscience.iop.org/0034-4885/70/4/R01/.
[Leroy and Rancoita (2016)] C. Leroy and P.G. Rancoita (2016), Principles of Radiation Interaction in Matter and Detection - 4th Edition -, World Scientific. Singapore, ISBN-978-981-4603-18-8 (printed); ISBN.978-981-4603-19-5 (ebook); https://www.worldscientific.com/worldscibooks/10.1142/9167#t=aboutBook; it is also partially accessible via google books.
[Lint, Flanahan, Leadon, Naber and Rogers (1980)] V.A. van Lint, T.M. Flanahan, R.E. Leadon, J.A. Naber and V.C. Rogers (1980), Mechanisms of Radiation Effects in Electronic Materials (New York: Wiley Interscience).
[Schroder (1997)] D.K. Schroder (1997), IEEE Trans. on Electron Devices ED-44, 160.
[Srour, Long, Millward, Fitzwilson and Chadsey (1984)] J.R. Srour, D.M. Long, D.G. Millward, R.L. Fitzwilson and W.L. Chadsey (1984), Radiation Effects on and Dose Enhancement of Electronic Materials (Park Ridge: Noyes Publications).
[Srour and McGarrity (1988)] J.R. Srour and J.M. McGarrity (1988) Proc. of the IEEE, Vol. 76 (Issue 11), 1443.
[Srour, Othmer and Chiu (1975)] J.R. Srour, S. Othmer and K.Y. Chiu (1975), IEEE Trans. on Nucl. Sci. 22 (no. 6), 2656.
[Vavilov and Ukhin (1977)] V.S. Vavilov and N.A. Ukhin (1977), Radiation Effects in Semiconductors and Semiconductor Devices (New York: Consultants Bureau, a division of Plenum Publishing Press).
1The linear dependence on the particle fluence [see Eq. (1)] is expected as long as the steady-state Fermi level is not moved significantly.
2A coefficient that is the reciprocal of that given in Eq. (1) is also found in literature (e.g., see Section 7.2.1 of [Lint, Flanahan, Leadon, Naber and Rogers (1980)] and references therein).
3For high-resistivity silicon (see discussion in Section 7.4.5 of [Leroy and Rancoita (2016)]), it was found that there are secondary defects whose concentrations are not linearly dependent on fluence.