The current web calculator for electronic stopping power exploits a fitted function on the tabulated data from ESTAR code at NIST, based on ICRU Report 37. The fitting function is a polynomial of degree 15 and the tables are reproduced with a maximum discrepancy < 1%.
The radiative stopping powers are those evaluated in ESTAR (e.g., see webpage). The tables corresponding are reproduced with a maximum discrepancy < 1%.
In ESTAR webpage at NIST, the uncertanties regarding the collision and radiative stopping power are discussed as reported in the following. The uncertainties of the calculated collision stopping powers for electrons are estimated (ICRU, 1984) to be 1 % to 2 % above 100 keV, 2 % to 3 % (in low-Z materials) and 5 % to 10 % (in high-Z materials) between 100 keV and 10 keV. The increasing uncertainties at low energies are due to the lack of shell corrections which are required when the velocity of the incident electron is no longer large compared to the velocities of the atomic electrons, especially those in the inner shells. Because of this limitation, tabulations of collision stopping powers are customarily restricted to energies above 10 keV. A similar restriction is recommended in regard to the use of the ESTAR. Due to the omission of shell corrections, the stopping powers from ESTAR are expected to be too large at very low energies. It is estimated that for materials of low atomic number, such as water, air or plastics, the error will be to the order of 10 % at 1 keV. ESTAR will not run below 1 keV. Radiative stopping powers are evaluated in ESTAR with a combination of theoretical bremsstrahlung cross sections described by Seltzer and Berger (1985). Analytical formulas (using a high-energy approximation) are used above 50 MeV, and accurate numerical results of Pratt et al. (1977) below 2 MeV. Cross sections in the intermediate energy region from 2 MeV to 50 MeV are obtained by interpolation, a procedure whose accuracy was confirmed by more detailed calculations for a few cases. The uncertainties of the radiative stopping powers are estimated to be 2 % above 50 MeV, 2 % to 5 % between 50 MeV and 2 MeV, and 5 % below 2 MeV.
The following link give access to the Web Applications for the Electronic Stopping Power for spectral fluence of Electrons:
How to use this Electronic Stopping Power Calculator and Ionizing Dose converter for spectral fluence
This tool calculates the spectral mass Electronic Stopping Power for a spectral fluence incident on a material.
The input parameters and options for the tool are described below. When the input form has been completed, pressing the "CALCULATE" button will start the calculation and open the "Results" page (allow for pop-up in your browser settings). The result page will be also linked at the bottom of the calculator page.
The conversion from mass electronic stopping power per unit area to dose is possible under the assumption that the energy lost by the incoming electron is fully absorbed by the medium - i.e., it is supposed to to be thick enough to fully absorb the kinetic energy of emitted delta rays - and the electron energy is almost constant while the particle traverses the absorber. In addition, radiative phenomema are assumed to be negligible - as, for instance, when the electron energy is well below that critical - e.g., see for a definition and a discussion Sect. 2.3.3.5 in Leroy and Rancoita (2016) and references therein -, and subsequent interactions of emitted photons are not taken into account. The discussion on the relevance of ionization energy loss (e.g, see Sects. 2.1-2.1.3.6 in Leroy and Rancoita (2016) and references therein) with respect to radiative emission of electrons can be found, for instance, in Sects. 3.1-3.1.3.3 and 3.2 of Leroy and Rancoita (2016) and references therein.
Input Parameters:
- Target material (Single Element or Compound)
- Spectral fluence.
Target Material
In the section "Target Selection" it is possible to specify a Single Element target material or a predefined Compound material. Fraction by weight, mean excitation energy and densities of media are available here.
Following is the maximum difference percentage between the fit and ICRU tables for single elements as a functions of the target atomic number (Z):
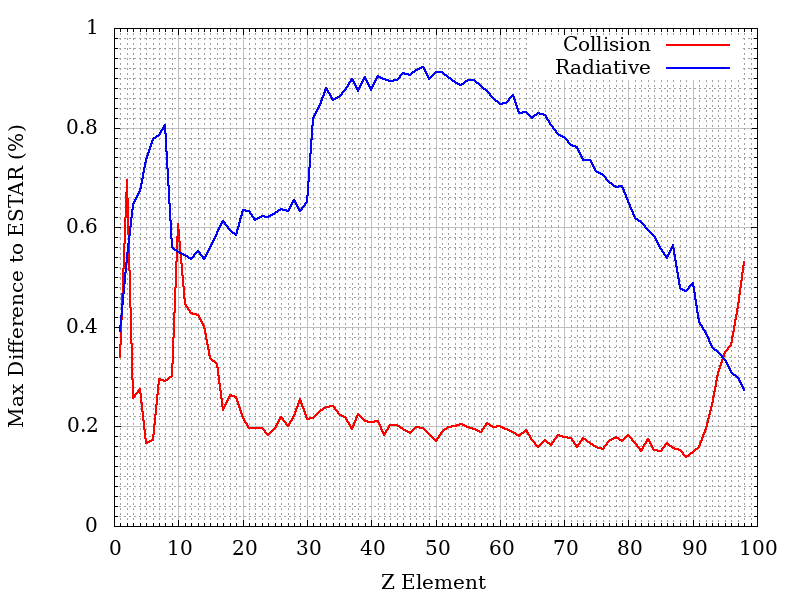
The overall max difference for compounds is 0.36% for collision, 0.91% for radiative. The average difference is 0.17% for collision and 0.73% for radiative.
Spectral Fluence
This section define the points of the spectral fluence as a function of energy.
The input format is one point per line (Energy - Flux , separated by a space or tab); it is also possible to copy and paste values. The minimum value of the particle spectral fluence is 1 keV, the maximum is 10 GeV.
Result
The result page contains the input spectral fluence and the Electronic Stopping Power curve in MeV cm2/g (i.e., the mass stopping power), calculated at the same energies defined in the spectral fluence. For every energy points the mass electronic stopping power per unit area and energy is calculated and displayed in the second graph. The mass electronic stopping power per unit area and energy is integrated at the energy steps defined in the spectral fluence and the results of every single bin is given in the last column of the table (mass electronic stopping power per unit area).
The upper energy limit of the last two column is set to that of the critical energy in the medium. It has to be remarked that critical energy vales are those available from particle data group (PDG) 2018 web page on Nuclear properties. These values - based on the remarks available at the critical energy webpage in PDG web site - are expected to differ from the actual ones by a few percents.