The current web calculator allows one to obtain the residual spectral fluence or residual energy of isotropically distributed protons and ions traversing a spherical shield by exploiting the "SRIM Module.exe" (with an upper energy limit of 5 GeV/amu) included in SRIM 2013 code (SRIM Tutorials) - whose maximum available energy is 10 GeV/amu -, i.e., the used electronic stopping power tables are those provided by "SRIM Module.exe" code with a low energy limit of 1 eV.
The probabilty distribution of path lenghts in the spherical absorber is obtained by means of a GEANT4 simulation.
The following link give access to the Web Applications for the calculation of the residual spectral fluence or residual energy of isotropically distributed protons and ions traversing a spherical absorber:
How to use this Calculator for particle spectral fluences or particle energy
For an incoming particle spectral fluence or particle energy isotropically distributed, this tool allows one to calculate the residual spectral fluence or residual energy in a point at distance r from the center of the sphere, with radius R, after traversing a spherical shielding material. The thickness of the spherical absorber is t.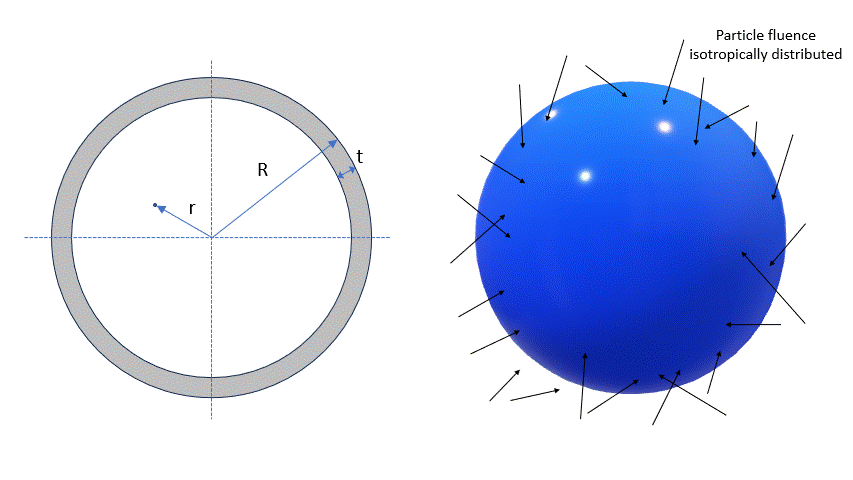
The input parameters and options for the tool are described below. When the input form has been completed, pressing the "CALCULATE" button will start the calculation and open the "Results" page (allow for pop-up in your browser settings). The result page will be also linked at the bottom of the calculator page.
Input Parameters:
- Input type
- Incident particle
- Target material
- Number of steps
- Shielding geometry
- Particle spectral fluence.
Input type
In the web Calculator, using the selector at the top of th calculator panel, the user can select the calculation of the residual spectral fluence or the residual energy for incoming protons or ions.
Spectral fluence is the default option: 
User has to change selection for mono-energetic particles:
Incident Particle
In the web Calculator, using the pull down menu, the user can select the species of incident particles, i.e., protons or any other elemental ions.
Except for the mass of protons and alpha particles, the user can also modify the mass (in amu) of the incident particle (e.g., for all isotopes one can refer to this page): the default mass is that of the most abundant isotope (MAI). Further information are available at the following webpage.
Target Material
In the section "Target Selection" it is possible to specify an User Defined target material or a predefined Compound material. User can also select the target as gas, this is allowed only for single element and natural gas target (H, He, N, O, F, Ne, Cl, Ar, Kr, Xe, Rn).
The stopping power in target gases is usually higher than that in an equivalent solid target. The Gas/ Solid correction disappears for higher velocity ions with energies above 2 MeV/amu. But at lower velocities the effect can be quite large - almost a 2 times change in stopping bacause of the Phase effect near the Bohr velocity, 25 keV/amu.
in the User Defined section individual elements can be selected as well as the composition of the target material choosing the number of elements in the compound. The required parameters for each element are:
- Atomic number (Z)/Chemical symbol
- Stoichiometric index or element fraction
Electronic Stopping Power for User Defined Compounds
Electronic Stopping Power for User Defined Compounds can be determined by means of Bragg's additivity rule, i.e., the overall Electronic Stopping Power in units of MeV cm2/g (i.e., the mass electronic stopping power) is obtained as a weighted sum in which each material contributes proportionally to the fraction of its atomic weight. For instance, in case of a GaAs medium ones obtains (e.g., Eq. (2.20) at page 15 in [ICRUM (1993)]):
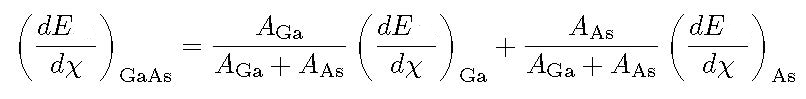
where ![]() and AGa [AAs] are the Electronic Stopping Power (in units of MeV cm2/g) and the atomic weight of Gallium [Arsenic], respectively.
and AGa [AAs] are the Electronic Stopping Power (in units of MeV cm2/g) and the atomic weight of Gallium [Arsenic], respectively.
As discussed in SRIM. (see help of "The Stopping and Range in Compounds" in SRIM-2013), the Compound Correction is usually zero for compounds containing heavy atoms, Al(Z>=13) or greater. All experiments with compounds such as Al2O3, SiO2, Fe2O3, Fe3O4, SiC, Si3N4, ZnO, and many more, show less than 2% deviation from Bragg's additivity rule which estimates the stopping by the sum of the stopping in the elemental constituents. That is, the stopping in Al2O3 is the same as the sum of the stopping in 2 Al + 3 O target atoms. For these compounds there is no need for a Compound Correction. This correction should be accounted for in compounds containing mostly H, C, N, O and F for ion stopping below 2 MeV per atomic mass unit and is negligible above 5 MeV per atomic mass unit. In the current calculator, no correction is applied for target atoms lighter than Al. Further details are available at SRIM Compound, and SRIM Compound Theory.
Predefined compounds
In the Compoud section it is possible to select a predefined compound including the SRIM compound corrections in the stopping power calculation.
For instance, in the following plot, it is shown the percentage difference of the stopping power of H2O (selected as User Defined material) and Water_Liquid (selected as a Compound) as a function of the incoming proton energy in MeV: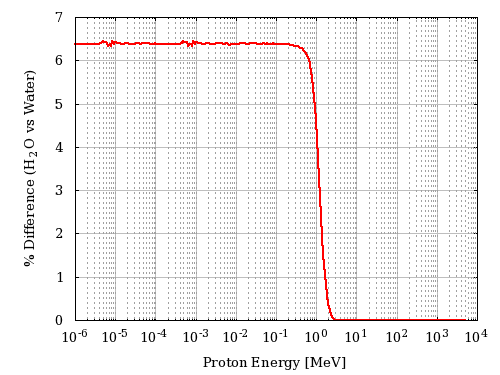
The default density value for each material is the one provided by SRIM code.
Number of Steps
In the web Calculator, using the pull down menu, the user can select the number of steps of the calculation - i.e., the traversed path is divided by the number of the steps.
The results of each steps is used as input for the following one to obtain the final result for the total traversed path.
In each step, the minimum traversed path is equivalent to about 5 μm of Si (1.16x10-3 [g cm-2]), e.g., 0.96 cm in Dry Air at sea level with density equal to 1.20484x10-3 g/cm3 (as implemented in SRIM from ICRU-37 table 5.5). The number of steps will be accordingly modified to keep each step above the minimum.
Shielding geometry
In this section users can modify the external sphere radius (R), the thickness of the shield (t) and the distance from the center of the sphere (r). The lower limit of traversed path is 5 μm.
Dependence of traversed path distribution on the distance (r) from the sphere center
In the following figure, the distribution of the traversed paths inside the shielding material are shown for a) r = 0 , b) r = D/2 , c) r = 0.95 D and d) r = D, where D = R - t where D = R - t with R = 50 cm, t= 0.127 cm of Al. The ditribution were obtained assuming that particles traverse the shielding material with their flight direction unchanged.
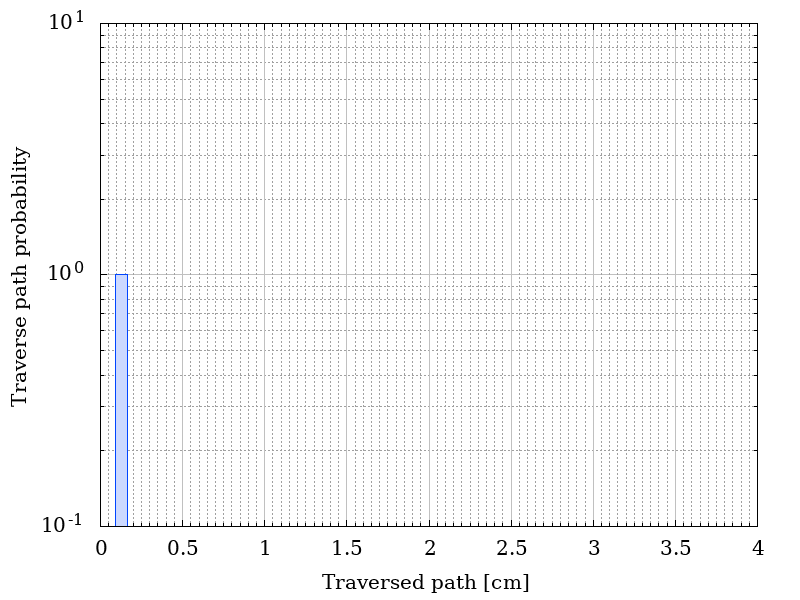
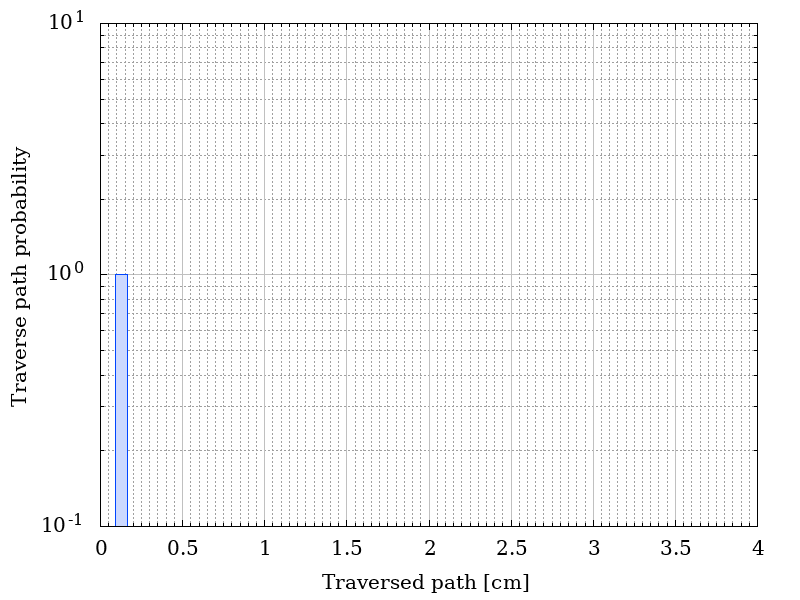
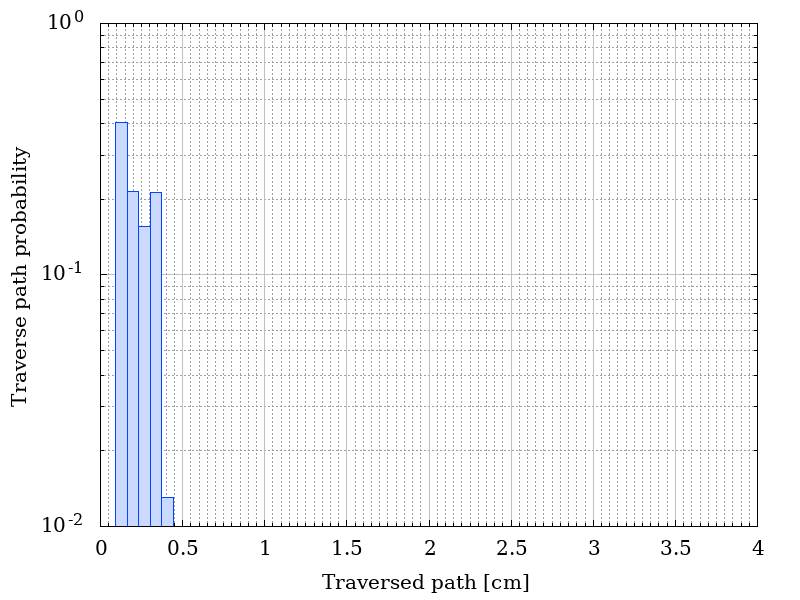
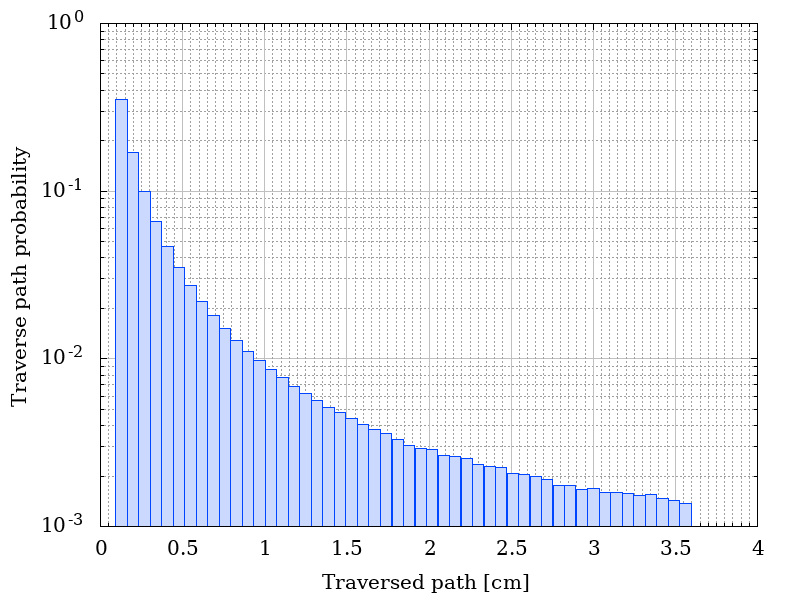
Traverse path probability as a functio of r.
The corresponding residual fluences are shown in the following figure. The incoming isotropical spectral flunece is listed here.
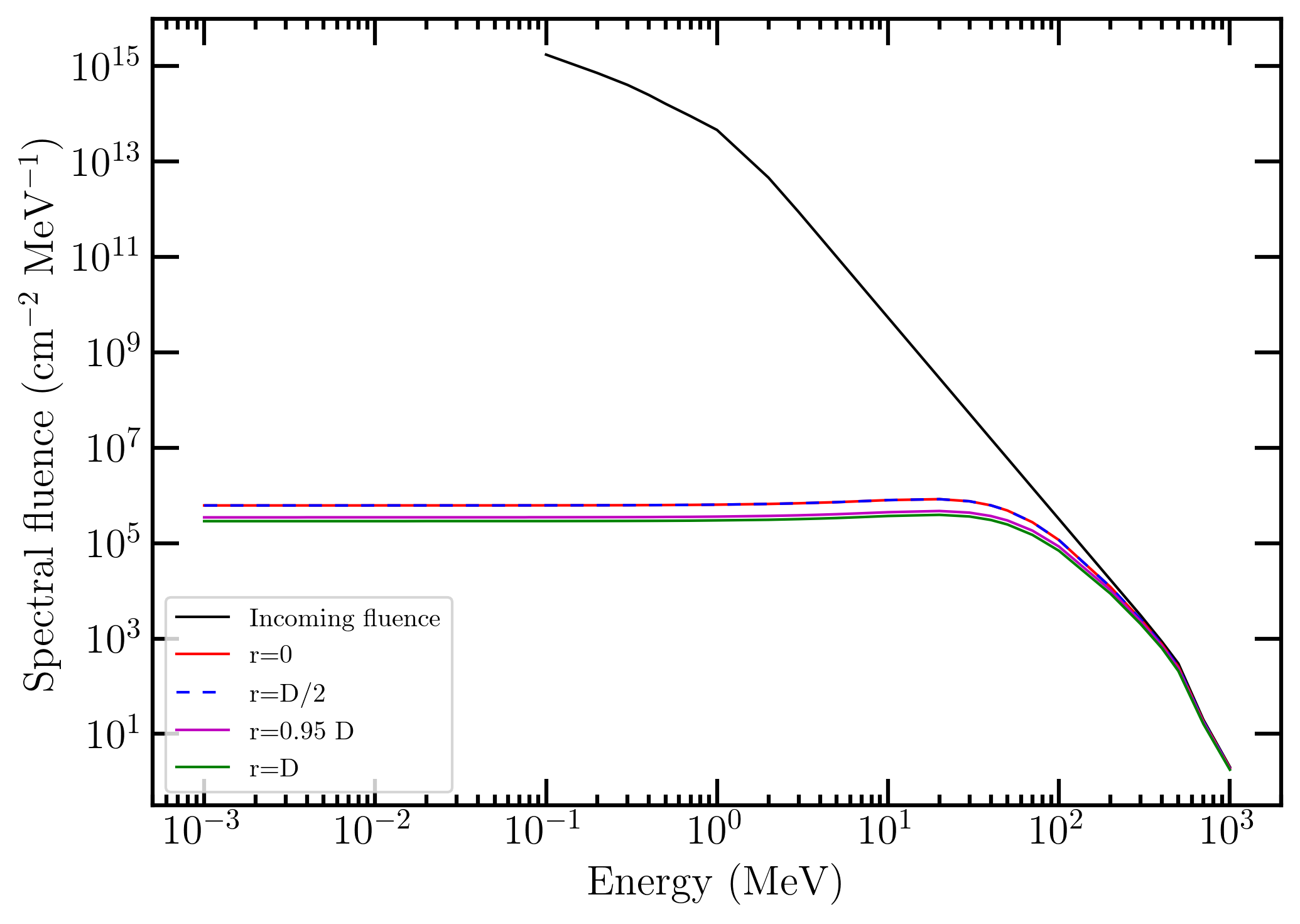
Incoming and residual spectral fluences as a function of r.
It has to be remarked that at r = 0 the residual spectral fluence is that obtained for a monodirectional spectral fluence impinging perpendicularly on a shielding material with thickness t. In fact, to rearch the sphere center, particles traverse the shielding material along radial directions thus resulting in traversed paths equal to the absorber thickness t.
In the following figure, the distribution of energies for 35 MeV of mono-energetic incoming protons with a fluence of 100 particles cm-2 are shown for a) r = 0 all protons have a residual energy of 3.0423e+01 MeV (no plot is shown), b) r = D/2 , c) r = 0.95 D and d) r = D, where D = R - t where D = R - t with R = 50 cm, t= 0.127 cm of Al. The ditribution were obtained assuming that particles traverse the shielding material with their flight direction unchanged.
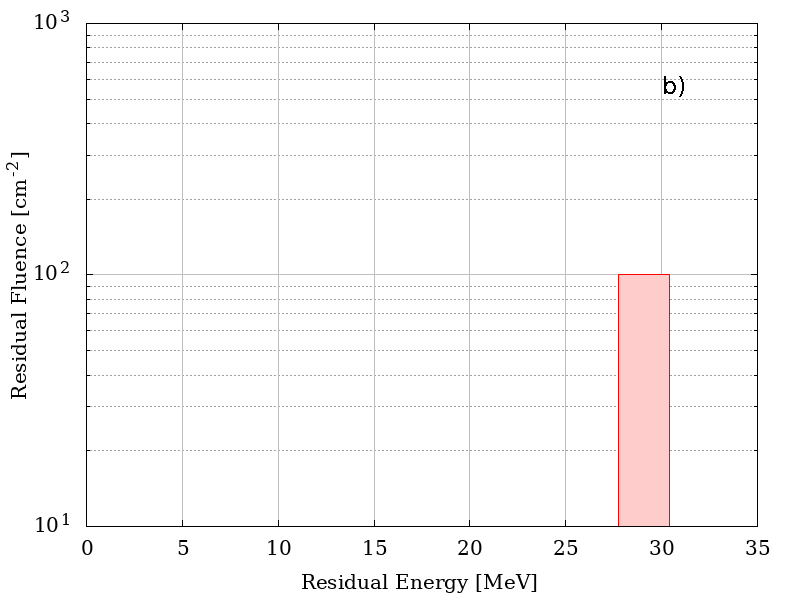
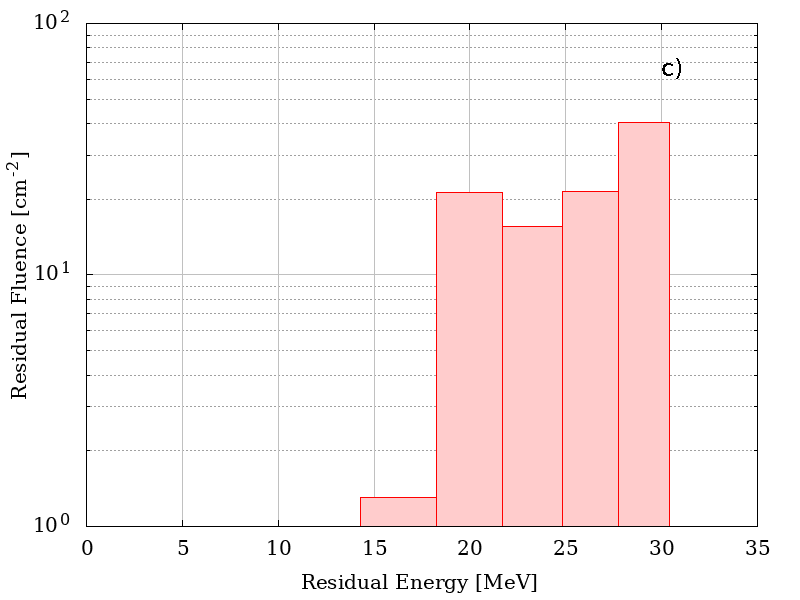
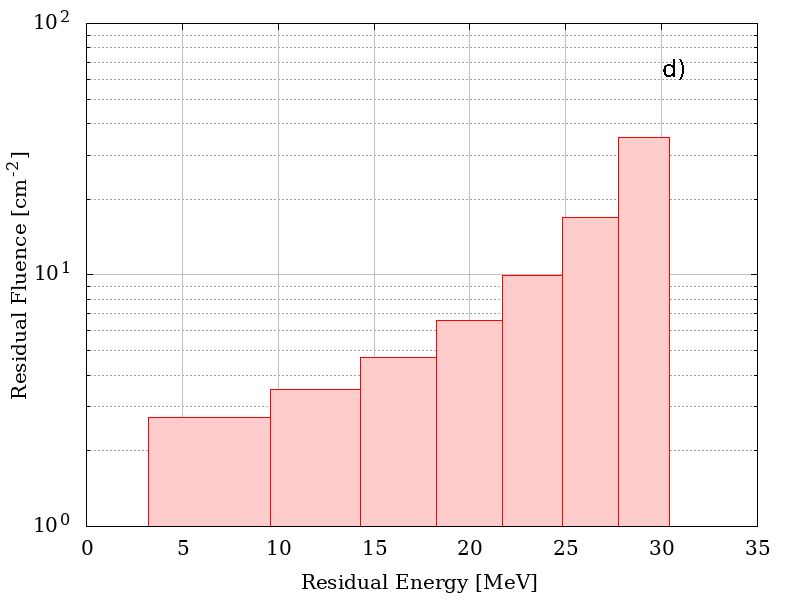
Residual energies as a functio of r.
Particle Spectral Fluence
This section define the points of the spectral fluence as a function of energy.
The input format is one point per line (Energy - Flux , separated by a space or tab); it is also possible to copy and paste values. The minimum value of the particle spectral fluence is 1 keV.
Mono-Energetic Particle
This section define the energy and fluence of the incoming protons or ions. The minimum value of the particle energy is 1 keV.
Result
In case of spectral fluence as input, the result page contains the graph of the input spectral fluence and the spectral fluence after traversing the absorber. The graph of the probability as a function of the traversed path is also provided. The table gives the values of the spectral fluence (above 1 keV) and the residual spectral fluence (above 1 keV) after traversing the absorber.
For mono-energetic particles the result page contains the graph of the distribution of energies after traversing the absorber. The graph of the probability as a function of the traversed path is also provided. The table gives the values of the residual fluence (above 1 keV) and the residual spectral fluence (above 1 keV) after traversing the absorber for each bin generated accordingly to the distribution of the probability as a function of the traversed path.
Residual energies were obtained disregarding multiple scattering effect, i.e., directions of flight of emerging particles were unchaged with respect to those of impinging directions.