The current case study regards the impact on the expected number of single event effects (SEEs) occurring in a device, when both the physical mechanism dealt by means of the so-called restricted energy-loss treatment and time-dependent solar modulation models are combined together.
The unprecedented measurement aaccuracy of the AMS-02 experiment associated with data collected during more than a decade has significantly expanded our past knowledge of GCRs fluences at high energies, well beyond the corresponding tabulated values of the electronic stopping power from the SRIM code. Additionally, for particle energies approaching or above the ionization minimum, the actually deposited energy in a medium may be lower than that dealt from the electronic stopping power due to emitted delta-rays not being fully absorbed (i.e., the restricted energy-loss has to be accounted for). At very high energy, this effect cannot be neglected anymore (e.g., see Particle flux per unit area as a function of particle energy or electronic stopping power/restricted energy loss per unit length, and relevance of solar modulation effects and Restricted energy-loss for cumulative (e.g., TID) and non-cumulative (e.g., SEE) energy deposition effects within SR-framework). Currently, the SR-NIEL website includes the so-called SR-framework electronic stopping power treatment, which extends the energy ranges covered by SRIM up to ultra-high energies. The related web calculators are available in the section Electronic Stopping Power Calculators (and TID doses) for protons, ions and electrons; Radiative Stopping Power for electrons. A further web calculator section is dedicated to Restricted Energy-Loss (and TID doses) Calculators within SR-framework of electronic stopping poweRestricted Energy-Loss (and TID doses) Calculators within SR-framework of electronic stopping power.
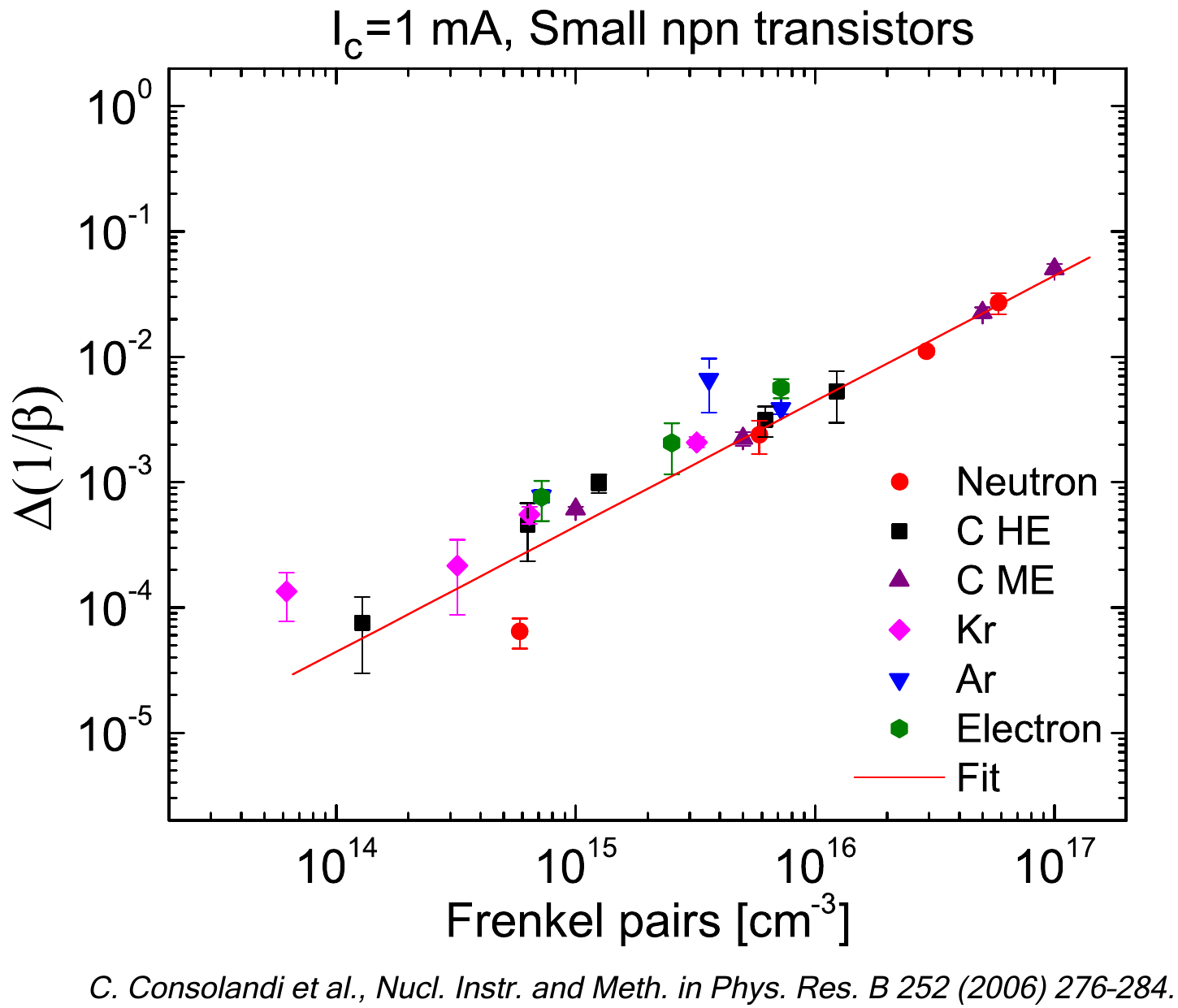
For the current case study, the expected number (S) for SEEs is computed for a Rad-hard 14-bit 400MSPS D/A converter (i.e., the part type DAC5675A discussed in [HIREX (2010)]) and it is based on the SEE cross section as a function of the mass electronic stopping power from HIREX (2010). In [HIREX (2010)], the SEE cross section for the part type DAC5675A (shown in Figure 5 at full scale current of 5 mA) is expressed by means of a four parameters Weibull function (for the formal equation see, for instance, Sect. 7 of [HIREX (2010)] and the discussion in Sect. 11.4.8.1 of [Leroy and Rancoita (2016)]) as a function of "LET" in MeV cm2 mg-1. The four parameters of the Weibull function at full scale current of 5 mA are reported in Table 2 of [HIREX (2010)]. The SEE cross section measurements were carried with N-, Ne-, Ar-, Fe-, Kr and Xe-ions at about (9.3-9.4) MeV/nucleon. It has to be remarked that, in this webpage, the unrestricted linear energy transfer - i.e., the electronic stopping power (as discussed in this webpage, see also [ICRU-85 (2011)]) - is indicated with the term "LET" in units of [MeV cm2 g-1] (e.g., see Section 2 of [ESCC-25100 (2014)]).
As discussed previously, since a device is usually not thick enough to fully absorb secondary δ-rays, the energy loss suffered by the incoming particle differs from the one deposited inside the traversed medium. As a consequence, the escaped δ-rays result in an effective detectable maximum transferred energy (indicated as W0 in the following) and, in turn, the energy deposition will reach a constant value, called the Fermi plateau at very high energy. Thus, when the energy deposited into an absorber or a device has to be considered, one has to deal with the so-called restricted energy loss - for instance, see the treatment by Fano (1963) - in which the effective detectable maximum transferred energy is accounted for (e.g., see Sect. 2.1.1.4 in [Leroy and Rancoita (2016)]). Finally, it has to be remarked that the electronic stopping power accounts for the energy lost by the incoming particle. In this webpage, it was already treated how, in general, a) the usage of restricted energy-loss is appropriate to account for the deposited energy and b) may result in lower number of expected SEEs with respect to that estimated when the energy loss by a particle is taken into account.
A further effect (discussed in this webpage) was investigated, i.e. that due to the time-dependent solar modulation which affects the omni-directional intensities of galactic cosmic rays (GCRs) species. In particular, five solar modulation model were considered:
- CREME version 96 [CREME (1996)] and version 2009 (e.g., see [CREME (2012)]) using the CREME FLUX module as available from CREME website upon registration;
- ISO-15390 model (e.g., see [ANSI (2004)]) using the package for galactic cosmic ray models as available from SPENVIS website upon registration;
- ISO(-15390)-DLR model (e.g., see [Matthiä et al (2013)]) using the web calculator as available from helmod.org website;
- HelMod (2019a) model using the web calculator as available from helmod.org website (e.g., see [HelMod (2019b)]).
HelMod - used within SR-framework - is a well-known Monte Carlo code developed to describe the transport of GCRs through the heliosphere from the interstellar space down to the Earth. Furthermore, the join GalProp-HelMod (2016) effort allowed one to determine local interstellar spectra (LIS) of protons, antiprotons, ions and electrons (e.g., [HelMod (2019a)]).
For the current case study, Fe-ions spectral fluences in units of [cm2 MeV]-1 were obtained, at 1 AU, for Carrington rotations (CR) 2148 (March 11, 2014 - April 7, 2014) and 2190 (April 29, 2017 - May 26, 2017) with solar conditions close to those of AMS-02 proton observations regarding the Bartels rotations 2464 (March 6, 2014 - April 1, 2014) and 2506 (April 13, 2017 - May 9, 2017) and discussed in this webpage. As illustrated here, CR2148 (CR2190) occurs during high solar activity (low solar activity). The CR duration is 2 356 992 s. In Figure 1 and 2, the spectral fluences of the investigated modulation models at 1 AU are shown from about 2.49 GeV, i.e., from 0.11 GeV above the kinetic energy threshold for allowing an Fe-ion to emerge, when the incoming particle strikes perpendicularly an Al absorber with a thickness of 50 mils (see the discussion in this webpage).
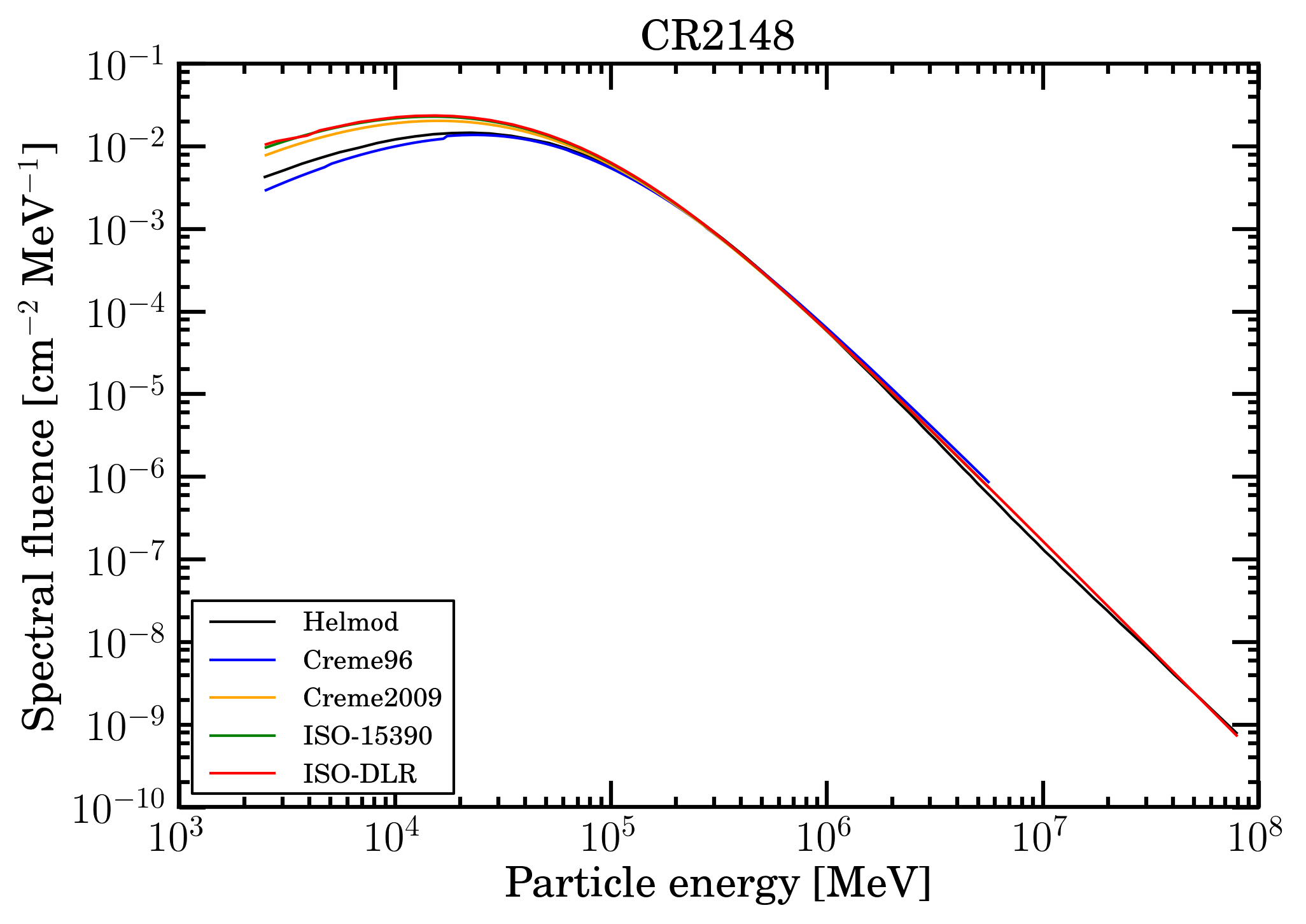
Figure 1. Fe-ion spectral fluences at 1AU as a function of the ion energy in MeV from 2.49 GeV for CR2148 for the presently investigated modulation models: CREME96 (blue curve), CREME2009 (orange curve), ISO-15390 (green curve), ISO-DLR (red curve) and HelMod (black curve).
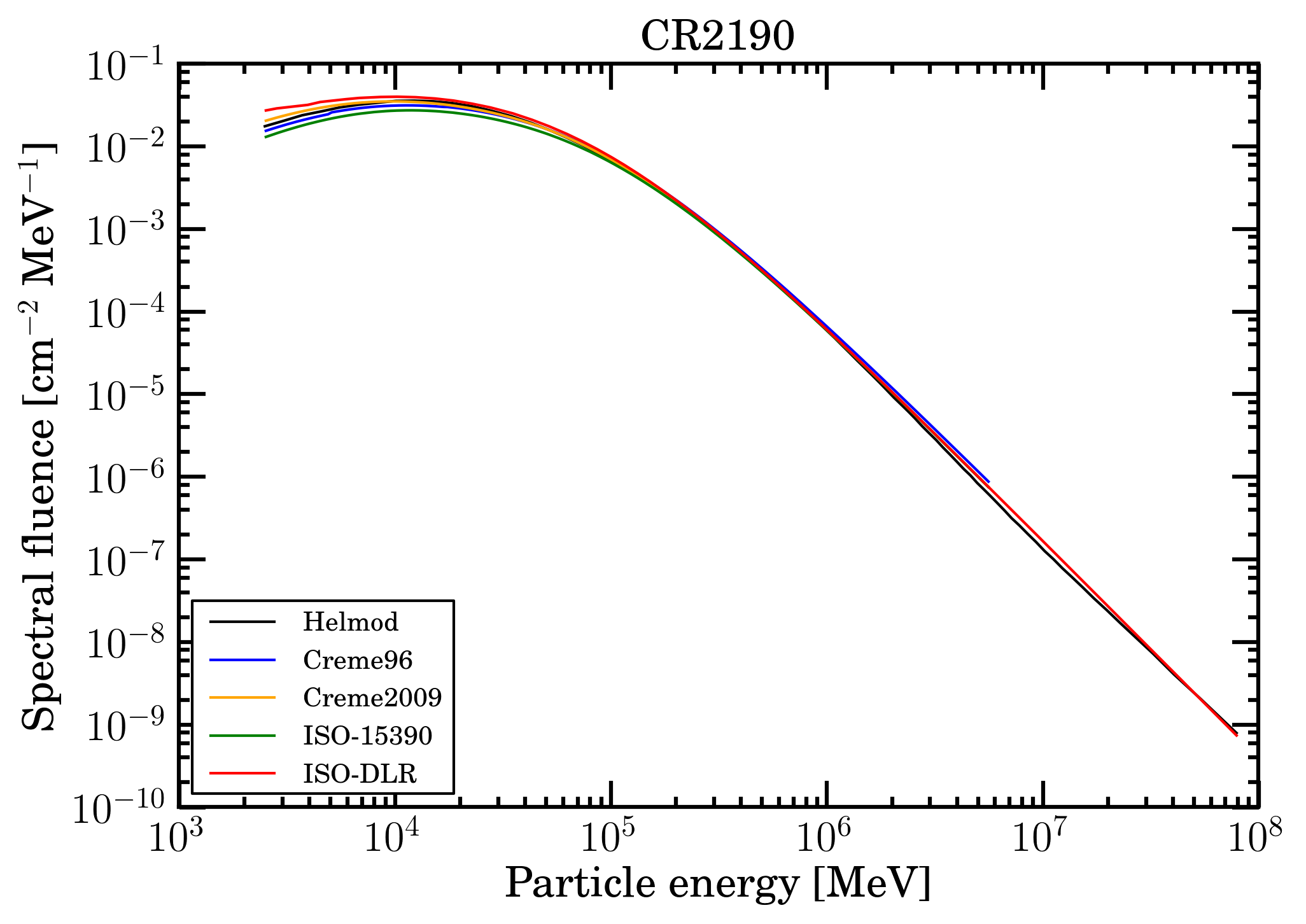
Figure 2. Fe-ion spectral fluences at 1AU as a function of the ion energy in MeV from 2.49 GeV for CR2190 (upper panel) for the presently investigated modulation models: CREME96 (blue curve), CREME2009 (orange curve), ISO-15390 (green curve), ISO-DLR (red curve) and HelMod (black curve).
Furthermore, in the following we will consider the particles as impinging perpendicularly on the front side of the absorbing medium for estimating both a) the residual Fe-ion fluences (shown in Figures 3 and 4 for CR2148 and CR2190, respectively) after traversing an Al absorber with a thickness of 50 mils and b) the number of expected SEEs.
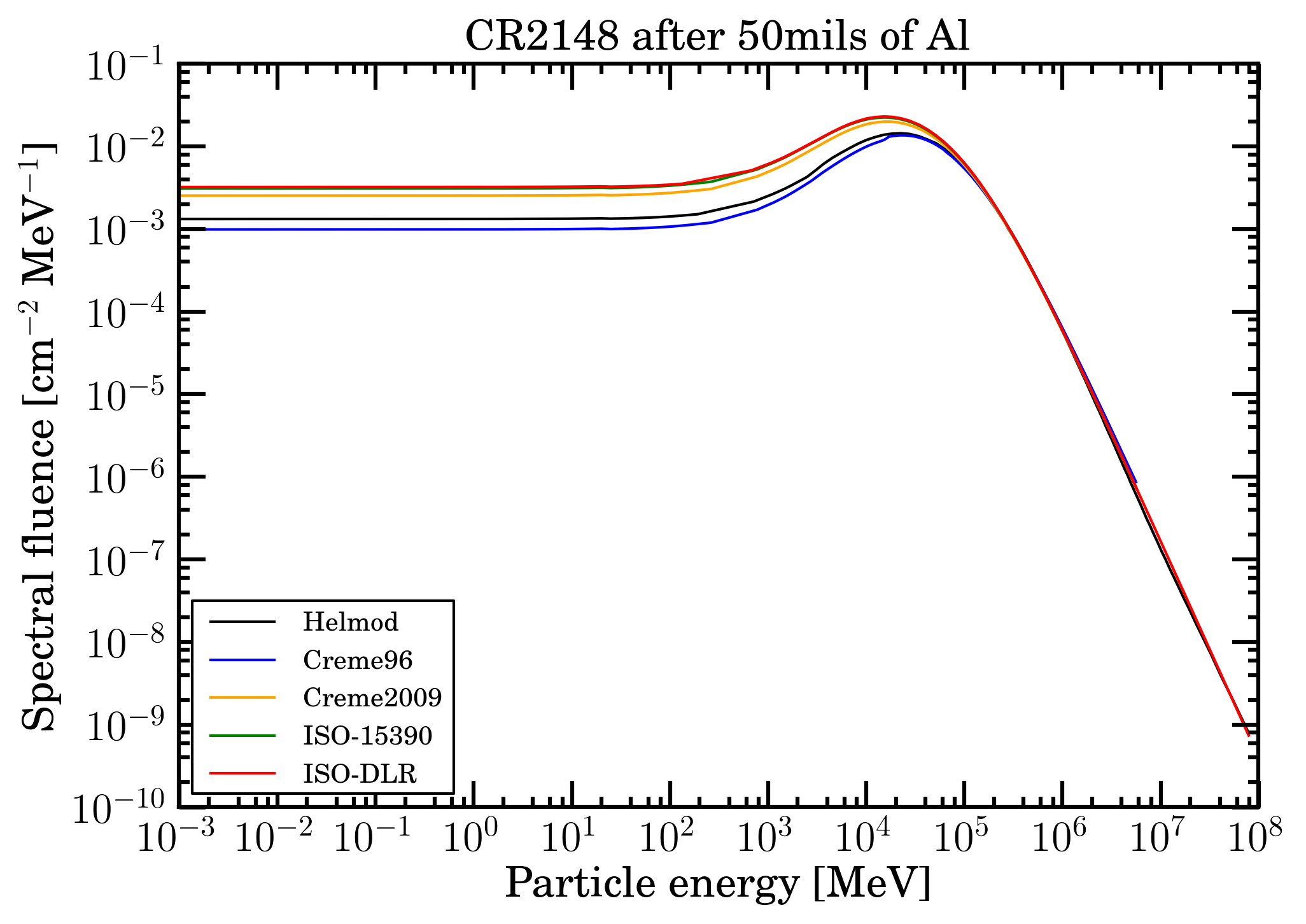
Figure 3. Fe-ion residual spectral fluences at 1AU as a function of the ion energy in MeV for CR2148 for the presently investigated modulation models: CREME96 (blue curve), CREME2009 (orange curve), ISO-15390 (green curve), ISO-DLR (red curve) and HelMod (black curve); they were obtained using an sr-niel calculator.
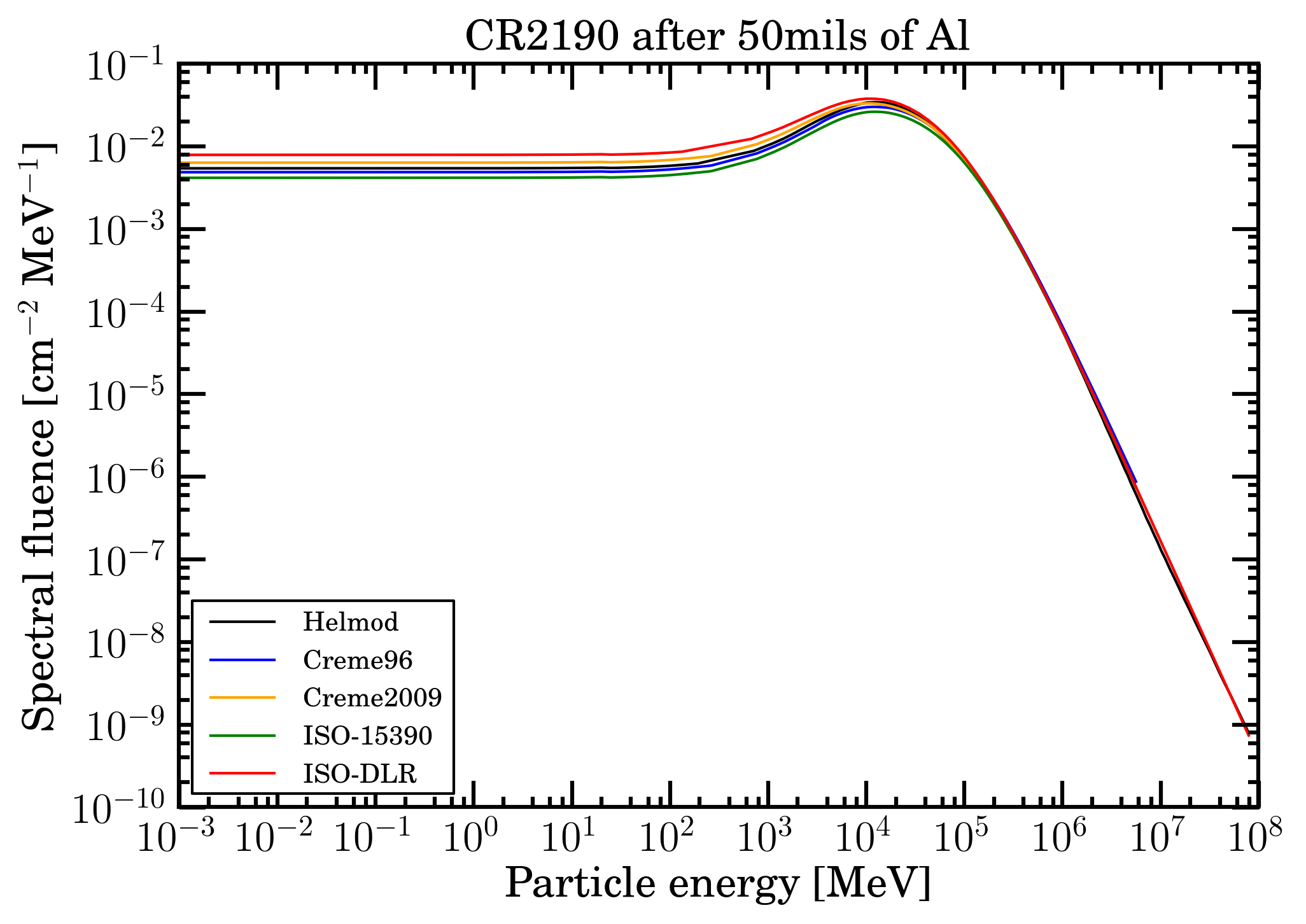
Figure 4. Fe-ion residual spectral fluences at 1AU as a function of the ion energy in MeV for CR2148 for the presently investigated modulation models: CREME96 (blue curve), CREME2009 (orange curve), ISO-15390 (green curve), ISO-DLR (red curve) and HelMod (black curve); they were obtained using an sr-niel calculator.
The expected number S of SEEs during Carrington rotations 2148 and 2190 was computed as:
![]() (1)
(1)
where Φ(E) is the spectral fluence (e.g., see Figures 1- 4) for the investigated solar modulation models, and σi(E) is the SEE cross section for the part type DAC5675A at full scale current of 5 mA [HIREX (2010)] as function of ion-energy with i= SR-framework mass electronic stopping power, mass restricted energy loss for W0=30, 300 keV; σi(E) was obtained using the SEE cross section, σ(LET), as a function of the mass electronic stopping power from HIREX (2010) using the methodology discussed in this webpage. Furthermore, Eq. (1) was computed for energies above 2.49 GeV for particle in free space and above 1 keV for particle emerging from an an Al absorber with a thickness of 50 mils.
In Tables 1 and 2, the value of the parameter S computed using Eq. (1) are reported as a function of solar modulation model (during CR2148 and CR2190) or the Fe-ion spectral fluences in free space and after traversing an Al absorber with a thickness of 50 mils, respectively.
| Model | CREME96 | CREME2009 | ISO-15390 | ISO-DLR | Helmod | |||||
| CR2148 | CR2190 | CR2148 | CR2190 | CR2148 | CR2190 | CR2148 | CR2190 | CR2148 | CR2190 | |
| Stopping Power SR-framework |
0.151 | 0.278 | 0.200 | 0.293 | 0.218 | 0.244 | 0.223 | 0.329 | 0.162 | 0.292 |
| Restricted energy loss W0=300keV |
0.129 | 0.248 | 0.176 | 0.264 | 0.193 | 0.217 | 0.198 | 0.298 | 0.140 | 0.263 |
| Restricted energy loss W0=30keV |
0.105 | 0.203 | 0.143 | 0.216 | 0.158 | 0.178 | 0.161 | 0.244 | 0.113 | 0.215 |
Table 1. As a function of solar modulation model, number of SEEs (S) using the SR-framework mass electronic stopping power and the mass restricted energy loss for W0=30, 300 keV, for Fe-ions spectral fluences (see Figure 1 and 2) in free space during CR2148 and CR2190.
| Model | CREME96 | CREME2009 | ISO-15390 | ISO-DLR | Helmod | |||||
| CR2148 | CR2190 | CR2148 | CR2190 | CR2148 | CR2190 | CR2148 | CR2190 | CR2148 | CR2190 | |
| Stopping Power SR-framework |
0.157 | 0.299 | 0.211 | 0.318 | 0.232 | 0.262 | 0.237 | 0.358 | 0.168 | 0.314 |
| Restricted energy loss W0=300keV |
0.135 | 0.270 | 0.188 | 0.290 | 0.207 | 0.236 | 0.212 | 0.327 | 0.146 | 0.286 |
| Restricted energy loss W0=30keV |
0.110 | 0.224 | 0.155 | 0.242 | 0.172 | 0.196 | 0.175 | 0.274 | 0.120 | 0.238 |
Table 2. As a function of solar modulation model, number of SEEs (S) using the SR-framework mass electronic stopping power and the mass restricted energy loss for W0=30, 300 keV, for Fe-ions spectral fluences (see Figure 3 and 4) after traversing an Al absorber with a thickness of 50 mils during CR2148 and CR2190.
By inspection of the Tables 1 and 2, one can remark that i) in particular, with respect to HelMod model, S (i.e., the expected number of SEEs) is slightly underestimated by CREME96, while the ISO-15390 model overestimates (underestimates) the expected number of SEEs during CR2148 (CR(2190) and ii) systematically the values of S increases by (3.7-12.1)% after the Fe-ions traverse an Al absorber with a thickness of 50 mils. As illustrated here, CR2148 (CR2190) occurs during high solar activity (low solar activity). Furthermore, by inspecting Table 2, the usage of the mass electronic stopping power results in larger expected numbers of SEEs with respect to those found when the restricted energy-loss is employed.
Bibliography
[ANSI (2004)] American National Standards Institute, Space environment (natural and artificial) – Galactic cosmic ray model (2004). Tech. Rep. ISO 15390, Washington, D.C.. Retrieved from https://www.iso.org/standard/37095.html.
[CREME (1996)] Tylka, A. J. et al. (1997). CREME96: A Revision of the Cosmic Ray Effects on Micro-Electronics Code, IEEE Trans. Nucl. Sci., 44, 2150-2160, 1997.; Badhwar, G.D. and O'Neill, P.M. (1996), Galactic cosmic radiation model and its applications, Ad. Sp. Res. 17, 7-17; and also: Badhwar, G.D. and O'Neill, P.M. (1992), An improved model of galactic cosmic radiation for space exploration missions, International Journal of Radiation Applications and Instrumentation. Part D. Nuclear Tracks and Radiation Measurements, Volume 20, Issue 3, 403-410, https://doi.org/10.1016/1359-0189(92)90024-P.
[CREME (2012)] Adams, J.H. et al. (2012). CRÈME: The 2011 Revision of the Cosmic Ray Effects on Micro-Electronics Code, IEEE Tran. Nucl. Scie. 59, 3141 - 3147.
[ESCC-25100 (2014)] SINGLE EVENT EFFECTS TEST METHOD GUIDELINES (2014). ESCC Basic Specification No. 25100 issue 2, available at https://escies.org/webdocument/showArticle?id=229
[Fano (1963)] Fano, U. (1963). Ann. Rev. of Nucl. Scie. 13, 1.
[GalProp-HelMod (2016)] GalProp-HelMod (2016). As advertised on the GALPROP website, HelMod website can be used as a service package to seamlessly calculate the effects of the heliospheric modulation for GALPROP output files. FROM GalProp homepage: "We are pleased to inform the community of the launch of a new service HelMod, which can be used to seamlessly calculate the effects of the heliospheric modulation for GALPROP output file".
[ICRU-85 (2011)] ICRUM - International Commission on Radiation Units and Measurements (2011). FUNDAMENTAL QUANTITIES AND UNITS FOR IONIZING RADIATION (Revised), ICRU Report 85, Journal of the ICRU Volume 11 No 1, https://doi.org/10.1093/rpd/ncs077
[HelMod (2019a)] Boschini, M. J. et al. (2019), The HelMod Model in the Works for Inner and Outer Heliosphere: from AMS to Voyager Probes Observations, Adv. Space Res., Available online 25 April 2019, in press, Accepted Manuscript, doi:10.1016/j.asr.2019.04.007 ArXiv:1903.07501.; see also Boschini, M. J. et al. (2018) HELMOD In The Works: From Direct Observations To The Local Interstellar Spectrum Of Cosmic-Ray Electrons Astrophys. J. 854(2):94, doi:10.3847/1538-4357/aaa75e; Boschini, M. J. et al. (2018) Deciphering the Local Interstellar Spectra of Primary Cosmic-Ray Species with HelMod. Astrophys. J. 858(1):61, doi:10.3847/1538-4357/aabc54; Boschini, M. J. et al. (2018), Propagation of Cosmic Rays in Heliosphere: the HelMod Model. Adv. Space Res., Volume 62, Issue 10, pages 2859-2879, 2018, doi:10.1016/j.asr.2017.04.017 ArXiv:1704.03733; Boschini, M. J. et al. (2017), Solution of Heliospheric Propagation: Unveiling the Local Interstellar Spectrum of Cosmic Rays Species Astrophysical Journal, 840:115, doi:10.3847/1538-4357/aa6e4f; Bobik et al. (2016), On the forward-backward-in-time approach for Monte Carlo solution of Parker's transport equation: One-dimensional case, Journal of Geophysical Research - Space Physics 121(5), 3920–3930, doi:10.1002/2015JA022237; Bobik, P. et al. (2012), Systematic Investigation of Solar Modulation of Galactic Protons for Solar Cycle 23 Using a Monte Carlo Approach with Particle Drift Effects and Latitudinal Dependence, Astrophys. J. 745:132, doi:10.1088/0004-637X/745/2/132.
[HelMod (2019b)] HelMod (2019b). The Fe-ion differential intensities were obtained from HelMod code [Ver. 4.0.0 - 01.May.2019] on Oct. 8 (2019). The Fe LIS (local interstellar spectrum) is not final and is based on current GalProp code normalization. At present, the Fe-LIS spectrum is under investigation by GalProp-HelMod (2016) join team and, possibly, an absolute scale decreasing of a few percents might be found.
[HIREX (2010)] HIREX (2010). Heavy Ion Test Report on part type DAC5675A - Rad-hard 14-bit 400MSPS D/A converter, Chip manufacturer: Texas Instruments -, report ref. HRX/SEE/0293, 26/7/2010.
[Leroy and Rancoita (2016)] C. Leroy and P.G. Rancoita (2016), Principles of Radiation Interaction in Matter and Detection - 4th Edition -, World Scientific. Singapore, ISBN-978-981-4603-18-8 (printed); ISBN.978-981-4603-19-5 (ebook); https://www.worldscientific.com/worldscibooks/10.1142/9167#t=aboutBook; it is also partially accessible via google books.
[Matthiä et al (2013)] Matthiä D., Berger T., Mrigakshi A. I., Reitz G. (2013), A ready-to-use galactic cosmic ray model, Advances in Space Research, Volume 51, Issue 3, Pages 329-338, https://doi.org/10.1016/j.asr.2012.09.022.