The occurance probability of events due to large energy depositions caused by a Coulomb interaction of the incoming particle in a device - like those commonly referred to as single event effects (SEE) – is usually expressed by means of the cross section as a function of mass electronic stopping power - or mass restricted energy loss - of the device material (e.g., see Sects. 11.4-11.4.9 of [Leroy and Rancoita (2016)] and references therein).
Thus, for a device whose thickness in g/cm2 is known along the particle path, one can determine a) the corresponding cross section as a function of the deposited energy in the device and, as a consequence, b) the overall occurrence probability due due to large energy deposition caused by recoil nuclei. In fact, for protons and ions traversing a medium the nuclear recoil energy deposition by ionization can be obtained using the recoil energy distribution (e.g., see this webpage) and the partition function from Robinson’s analytical approximation (e.g., see this webpage and this web calculator). For compounds, the Bragg's additivity rule is applied (see, for instance, this webpage).
One has to remark that the recoil energy is deposited by ionizing and non-ionizing processes. For every recoil energy value, the amounts of energy deposited for those processes are available, for elements, at Energy Partition Function Calculator. For further information about the computation method are available at the Nuclear Stopping Power for Electrons, Protons and Ions page.
For incoming protons and ions, the following link allows one to access the calculator for the Probability of events occurrence due to recoil of target nuclei in devices:
How to use this calculators for probability of events occurrence due to recoil of target nuclei in devices
This tool allows one to calculate the Probability of events occurrence due to the recoil of target nuclei in devices for incident particles with kinetic energy E traversing a material.
The mass electronic stopping power, dE/dχ in [MeV cm2 g-1] – on which the input SEE cross section (σSEE) ) is fuctionally dependent – provides the corresponding average energy deposited by ionization, <Eion>, for particles traversing a tickness d along the motion direction:
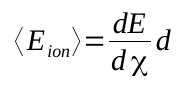
with d in [g cm-2].
For a particle with energy E, the probability to create a recoil with energy <Eion> deposited by ionization is obtained from (see also this webpage):
![]()
where nA is the number of atoms per cm3 in the absorber, t is the traversed thickness in cm, σtot(E, <Eion>) is the cross section for the occurrence of a recoil nucleus with deposited ionizating energy <Eion> in an energy bin dEion; σtot(E, <Eion>) is obtained following the sr-treatment. <Eion> is considered to be locally deposited and absorbed up to Emax, i.e., the effectrive maximun ionizing energy deposited and absorbed from the recoil nucleus inside the device medium due to its finite size.
<Eion> is related to the recoilt energy kinetic energy T by mean of the partition function L(T) (see also the webpage and calculator):
![]()
Finally, the number of SEE in each energy bin dE, centered at the energy <Eion>, is found as:
![]()
where F(E) is the particle fluence.
The overall number of SEE is obtained summing the contribution from each energy bin.
The input parameters and options for the tool are described below. When the input form has been completed, pressing the "CALCULATE" button will start the calculation and open the "Results" page (allow for pop-up in your browser settings). The result page will be also linked at the bottom of the calculator page.
Input Parameters:
- Incident particle
- Energy
- Fluence
- Device material and parameters
- Device thickness along the direction of incident particles
- Maximun ionizing energy deposited and absorbed from recoil nuclues
- SEE Cross section (Weibull function parameters)
Currently, as an example, the default parameters for the Weibull function are those for the device treated in this webpage.
Incident Particle
In the calculator panel, using the pull down menu, the user can select the species of the incident particle, either a proton or one of the elemental ions.
The user can also modify the mass (in amu) of the incident particle (e.g., for all isotopes one can refer to this page): the default mass is that of the most abundant isotope (MAI), except for proton and alpha particle masses. Further information are available at the following webpage.
Energy and Fluence
This section define the energy, in MeV, and the fluence, in cm-2, of the impinging particles.
Device Material and Parameters
In the section "Device Material Selection" it is possible to specify an User Defined device material or a predefined Compound.
in the User Defined section individual elements can be selected as well as the composition of the device material choosing the number of elements in the compound. The required parameters for each element are:
- Atomic number (Z)/Chemical symbol
- Stoichiometric index or element fraction
The differential probabilty in each ionization energy bin is obtained by means of Bragg's additivity rule, i.e., the overall value is obtained as a weighted sum in which each material contributes proportionally to the fraction of its atomic weight (see, for instance, this webpage).
Maximun ionizing energy deposited and absorbed by recoil nuclues
Such a quantity, indicated as Emax, accounts for the effectrive maximun ionizing energy deposited and absorbed from the recoil nucleus inside the device medium due to its finite size.
Device thickness along the direction of incident particles
This input value defines the device thickness along the direction of incident particles. The thickness is expressed in [g cm-2], i.e,:
(thickness in cm) x (absorber density in g cm-3) .
SEE Cross section
This section define parameters that are included in the Weibull function:
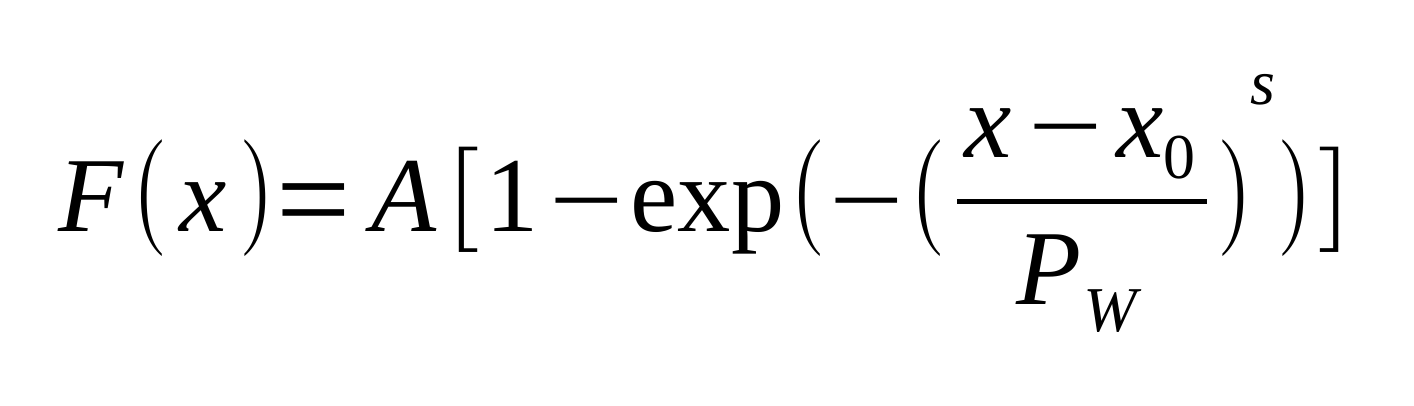
where x is the stopping power (or the restricted energy loss) in MeV cm2 mg-1, A is the saturation cross section, x0 is the stopping power (or LET) threshold parameter, PW is the width parameter and s is a dimensionless exponent.
Result
The result page contains the SEE cross section as a function of the mass electronic stopping power and as a function of average energy deposited by ionization <Eion>. The overall spectral recoil probability is also shown as a function of <Eion>. The spectral number of SEE as a function of <Eion> is shown in the third graph. In the table are reported the mentioned variables in 1000 bins of energy.